题目内容
直角三角形ABC的直角顶点A为动点,B(-
,0)C(
,0),作AD⊥BC于D,动点E满足
=(1-
)
,当动点A运动时,点E的轨迹为曲线G,
(1)求曲线A的轨迹方程;
(2)求曲线G的轨迹方程;
(3)设直线L与曲线G交于M、N两点,坐标原点O到直线L的距离为
,求|MN|的最大值.
| 3 |
| 3 |
. |
| AE |
| ||
| 3 |
. |
| AD |
(1)求曲线A的轨迹方程;
(2)求曲线G的轨迹方程;
(3)设直线L与曲线G交于M、N两点,坐标原点O到直线L的距离为
| ||
| 2 |
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由圆的性质可得:直角三角形ABC的直角顶点A的轨迹为圆.
(2)设E(x,y),A(x0,y0),则D(x0,0),由于动点E满足
=(1-
)
,可得
,解得x0=x,y0=
y,代入曲线A的轨迹方程即可得出.
(3)当直线L的斜率不存在时,直线L的方程为:x=±
,|MN|=
.
当直线L的斜率存在时,设直线L的方程为:y=kx+m,M(x1,y1),N(x2,y2).由于坐标原点O到直线L的距离为
,可得
=
.直线方程与椭圆的方程联立化为(1+3k2)x2+6kmx+3m2-3=0,利用根与系数的关系、弦长公式、基本不等式的性质即可得出|MN|的最大值.
(2)设E(x,y),A(x0,y0),则D(x0,0),由于动点E满足
. |
| AE |
| ||
| 3 |
. |
| AD |
|
| 3 |
(3)当直线L的斜率不存在时,直线L的方程为:x=±
| ||
| 2 |
| 3 |
当直线L的斜率存在时,设直线L的方程为:y=kx+m,M(x1,y1),N(x2,y2).由于坐标原点O到直线L的距离为
| ||
| 2 |
| |m| | ||
|
| ||
| 2 |
解答:
解:(1)直角三角形ABC的直角顶点A的轨迹为圆:x2+y2=3(x≠±
);
(2)设E(x,y),A(x0,y0),则D(x0,0),
+
=3,
∵动点E满足
=(1-
)
,
∴
,解得x0=x,y0=
y,
代入曲线A的轨迹方程可得x2+3y2=3,化为
+y2=1(x≠±
).
(3)当直线L的斜率不存在时,直线L的方程为:x=±
,|MN|=
.
当直线L的斜率存在时,设直线L的方程为:y=kx+m,M(x1,y1),N(x2,y2).
∵坐标原点O到直线L的距离为
,
∴
=
,化为4m2=3+3k2.
联立
,化为(1+3k2)x2+6kmx+3m2-3=0,
则x1+x2=
,x1x2=
.
又4m2=3+3k2.
∴|MN|=
=
=
≤
=2,当且仅当k2=
时取等号.
综上可得:|MN|的最大值为2.
| 3 |
(2)设E(x,y),A(x0,y0),则D(x0,0),
| x | 2 0 |
| y | 2 0 |
∵动点E满足
. |
| AE |
| ||
| 3 |
. |
| AD |
∴
|
| 3 |
代入曲线A的轨迹方程可得x2+3y2=3,化为
| x2 |
| 3 |
| 3 |
(3)当直线L的斜率不存在时,直线L的方程为:x=±
| ||
| 2 |
| 3 |
当直线L的斜率存在时,设直线L的方程为:y=kx+m,M(x1,y1),N(x2,y2).
∵坐标原点O到直线L的距离为
| ||
| 2 |
∴
| |m| | ||
|
| ||
| 2 |
联立
|
则x1+x2=
| -6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
又4m2=3+3k2.
∴|MN|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[
|
3+
|
3+
|
| 1 |
| 3 |
综上可得:|MN|的最大值为2.
点评:本题考查了圆的方程、椭圆的标准方程及其性质、弦长公式、点到直线的距离公式,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知A(x-2,
)、B(0,
)、C(x,y),若
⊥
,则动点C的轨迹方程为( )
| y |
| 2 |
| y |
| 2 |
| AC |
| BC |
| A、y2=8x |
| B、y2=-8x |
| C、y2=8(x-2) |
| D、y2=-8(x-2) |
 如图目标函数z=ax-y的可行域为四边形OAPB(含边界),若P(2,2)是该目标函数z=ax-y的唯一最优解,则实数a的取值范围是( )
如图目标函数z=ax-y的可行域为四边形OAPB(含边界),若P(2,2)是该目标函数z=ax-y的唯一最优解,则实数a的取值范围是( )| A、(-2,-1) | ||
B、[
| ||
C、[-1,-
| ||
D、(-1,-
|
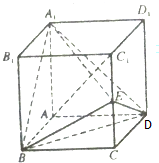 如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.
如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.