题目内容
5.${∫}_{0}^{1}$e-xdx=1-$\frac{1}{e}$.分析 根据定积分的法则计算即可.
解答 解:${∫}_{0}^{1}$e-xdx=-e-x|${\;}_{0}^{1}$=-($\frac{1}{e}$-1)=1-$\frac{1}{e}$,
故答案为:$1-\frac{1}{e}$
点评 本题考查了定积分的计算,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
15.设抛物线y2=2px的焦点在直线2x+3y-4=0上,则该抛物线的准线方程为( )
| A. | x=-1 | B. | x=-2 | C. | x=-3 | D. | x=-4 |
20.已知集合A={1,2,3,4,5},B={x∈Z|x≤2},则A∩B中的元素个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.已知函数f(x)=x2,x∈[2m,m+6]是偶函数,则实数m的值为( )
| A. | -4 | B. | -2 | C. | -1 | D. | 6 |
14.函数$y=lg|{x+1}|-\frac{1}{x}$的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
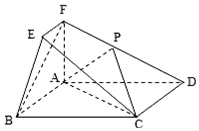 在如图所示的几何体中,四边形ABCD为矩形,平面ABCD⊥平面ABEF,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABCD⊥平面ABEF,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.