题目内容
15.设抛物线y2=2px的焦点在直线2x+3y-4=0上,则该抛物线的准线方程为( )| A. | x=-1 | B. | x=-2 | C. | x=-3 | D. | x=-4 |
分析 求出直线与x轴的交点坐标,得到抛物线的焦点坐标,然后求解抛物线的准线方程.
解答 解:抛物线y2=2px的焦点在直线2x+3y-4=0上,可得焦点坐标(2,0),
所求的抛物线的准线方程为:x=-2.
故选:B.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
10.若sinθ+cosθ=$\sqrt{2}$,则tanθ+$\frac{1}{tanθ}$=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
7.已知两条平行线l1:3x+4y-4=0与l2:ax+8y+2=0之间的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.某中学为了选拔优秀数学尖子参加本市举行的数学竞赛,先在本校甲、乙两个实验班中进行数学能力摸底考试,考完后按照大于等于90分(百分制)为优秀,90分以下为非优秀,统计成绩后,得到如下所示2×2列联表
附公式:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
已知在全部105人中随机抽取1人为优秀的概率为$\frac{2}{7}$
( I)请完成上面的列联表中未填数据,并按95%的可靠性要求,你能否认为学生的成绩与班级有关系?
( II)若按分层抽样方法抽取甲、乙两班优秀学生9人,然后再选派3人参加市里的数学竞赛,记甲班优秀生被派出的人数为x,试求x的分布列及数学期望.
| 优秀 | 非优秀 | 总计 | |
| 甲班 | a=10 | b=45 | a+b=55 |
| 乙班 | c=20 | d=30 | c+d=50 |
| 合计 | a+c=30 | b+d=75 | 105 |
| P(x2>k) | 0.010 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.82 |
( I)请完成上面的列联表中未填数据,并按95%的可靠性要求,你能否认为学生的成绩与班级有关系?
( II)若按分层抽样方法抽取甲、乙两班优秀学生9人,然后再选派3人参加市里的数学竞赛,记甲班优秀生被派出的人数为x,试求x的分布列及数学期望.
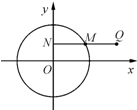 如图,已知点M在圆O:x2+y2=4上运动,MN⊥y轴(垂足为N),点Q在NM的延长线上,且|QN|=2|MN|.
如图,已知点M在圆O:x2+y2=4上运动,MN⊥y轴(垂足为N),点Q在NM的延长线上,且|QN|=2|MN|.