题目内容
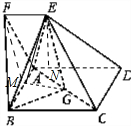
 如图,四边形ABCD为矩形,四边形ADEF为梯形,FE
如图,四边形ABCD为矩形,四边形ADEF为梯形,FE
| ||
. |
| 1 |
| 2 |
(Ⅰ)求证:EG∥平面ABF;
(Ⅱ)求三棱锥B-AEG的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)取AB的中点M,连FM,GM,先证明出四边形GMFE为平行四边形,进而推断出EG∥FM,最后由线面平行的判定定理证明出EG∥平面ABF.
(Ⅱ)先作出三棱锥的高EN,通过证明出∠EAD=60°,求得AE,然后求得三角形BAG的面积,最后根据棱锥体积公式求得答案.
(Ⅱ)先作出三棱锥的高EN,通过证明出∠EAD=60°,求得AE,然后求得三角形BAG的面积,最后根据棱锥体积公式求得答案.
解答:
(Ⅰ)证明:取AB的中点M,连FM,GM,
∵G为对角线AC的中点,
∴GM∥AD,且GM=
AD,
∵EF∥AD,
∴MG∥EF,且EF=GM,
∴四边形GMFE为平行四边形,
∴EG∥FM,
∴EG∥平面ABF.
(Ⅱ)作EN⊥AD,垂足为N,
由平面ABCD⊥面AEFD,面ABCD∩面AEFD=AD,
∴EN⊥面ABCD,即EN为三棱锥E-ABG的高,
∵在△AEF中,AF=FB,∠AFE=60°,
∴△AEF是正三角形,
∴∠AEF=60°,
由EF∥AD,知∠EAD=60°,
∴EN=AE•sin60°=
,
MG=
AD=EF=2,
∴S△ABG=
×2×2=2,
∴三棱锥B-AEG的体积为:
×2×
=
.
∵G为对角线AC的中点,
∴GM∥AD,且GM=
| 1 |
| 2 |
∵EF∥AD,

∴MG∥EF,且EF=GM,
∴四边形GMFE为平行四边形,
∴EG∥FM,
∴EG∥平面ABF.
(Ⅱ)作EN⊥AD,垂足为N,
由平面ABCD⊥面AEFD,面ABCD∩面AEFD=AD,
∴EN⊥面ABCD,即EN为三棱锥E-ABG的高,
∵在△AEF中,AF=FB,∠AFE=60°,
∴△AEF是正三角形,
∴∠AEF=60°,
由EF∥AD,知∠EAD=60°,
∴EN=AE•sin60°=
| 3 |
MG=
| 1 |
| 2 |
∴S△ABG=
| 1 |
| 2 |
∴三棱锥B-AEG的体积为:
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
点评:本题主要考查了线面平行和线面垂直的判定定理的应用,棱锥体积的计算公式.考查了学生综合的观察能力和思维能力.

练习册系列答案
相关题目
在等边△ABC的边BC上任取一点p,则S△ABP≤
S△ABC的概率是( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,PD=2,E为AB的中点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,PD=2,E为AB的中点.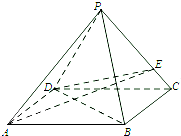 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2