题目内容

在△ABC中，求证：
a=bcosC+ccosB，
b=ccosA+acoaC，
c=acoaB+bcosA．
考点：正弦定理
专题：证明题,解三角形
分析：由正弦定理，可得，a=2rsinA，b=2rsinB，c=2rsinC，再由诱导公式和两角和的正弦公式，即可证得．
解答： 证明：由正弦定理，
a
sinA
=
b
sinB
=
c
sinC
=2r，（r为△ABC的外接圆的半径）
则a=2rsinA，b=2rsinB，c=2rsinC，
则a=2rsinA=2rsin（B+C）=2r（sinBcosC+cosBsinC）
=2rsinBcosC+2rsinCcosB=bcosC+ccosB；
b=2rsinB=2rsin（A+C）=2r（sinAcosC+cosAsinC）
=2rsinAcosC+2rsinCcosA=acosC+ccosA；
c=2rsinC=2rsin（A+B）=2r（sinAcosB+cosAsinB）
=2rsinAcosB+2rsinBcosA=acosB+bcosA．
即有等式成立．
点评：本题考查正弦定理及运用，考查诱导公式和两角和的正弦公式的运用，考查推理能力，属于基础题．
练习册系列答案
相关题目
 如图，四棱锥E-ABCD中，底面ABCD是梯形，且AB∥CD，2AB=3CD，点F是线段EA上的点，且EC∥平面BDF，则
EF
EA
等于（　　）
A、
2
3
B、
2
5
C、
1
2
D、
1
3
设图F1、F2分别为双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左、右焦点，双曲线上存在一点P使得|PF1|+|PF2|=3b，|PF1|•|PF2|=
9
4
ab，则该双曲线的离心率为（　　）
A、
4
3
B、
5
3
C、
9
4
D、3
设函数f（ex）=ex，g（x）=
1
e
f（x）-（x+1）（e=2.718…）
（1）求函数g（x）的极大值
（2）求证1+
1
2
+
1
3
+…+
1
n
＞ln(n+1)(n∈N*)
（3）若h（x）=
1
2
x2，曲线y=h（x）与 y=f（x）是否存在公共点，若存在公共点，在公共点处是否存在公切线，若存在，求出公切线方程，若不存在，说明理由．
不等式16x-logax＜0在(0，
1
4
)恒成立，则实数a的取值范围（　　）
A、(
1
4
，1)
B、(
1
2
，1)
C、[
1
2
，1)
D、[
1
4
，1)
如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．
（Ⅰ）证明：D1E⊥A1D；
（Ⅱ）当E为AB的中点时，求点E到面ACD1的距离；
（Ⅲ）在（Ⅱ）的条件下，求D1E与平面AD1C所成角的正弦值．
已知数列{an}的前n项和为Sn，且{
1
an
}是等差数列，公差d＞0，a1=
1
2
，S3=
13
12
，函数f（x）=
x
1+x
-ln（1+x）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：f（an）＜0（n∈N*）；
（Ⅲ）求证：sn＜ln（1+n）对一切正整数n都成立．
已知等差数列{an}满足：a2=5，a4+a6=22
（Ⅰ）求an；
（Ⅱ）若f（x）=
1
x2-1
，bn=f（an）（n∈N*），求数列{bn}的前n项和Tn．
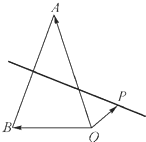如图，P为△AOB所在平面内一点，向量
OA
=
a
，
OB
=
b
，且点P在线段AB的垂直平分线上，向量
OP
=
c
．若|
a
|=3，|
b
|=2，则
.
c
•(
a
-
b
)的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网