题目内容
71与19的最大公约数是( )
| A、19 | B、7 | C、3 | D、1 |
考点:用辗转相除计算最大公约数
专题:算法和程序框图
分析:利用“辗转相除法”即可得出.
解答:
解:∵71=19×3+14,
19=14+5,
14=5×2+4,
5=4+1,而4与1互质,
∴71与19的最大公约数是1.
故选:D.
19=14+5,
14=5×2+4,
5=4+1,而4与1互质,
∴71与19的最大公约数是1.
故选:D.
点评:本题考查了“辗转相除法”,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
“a=4”是“函数f(x)=x2+ax+1在区间[-2,+∞)上为增函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列不等式中不成立的是( )
| A、50.5<60.5 |
| B、log32<0.1-0.2 |
| C、log23<log25 |
| D、0.10.3<0.10.4 |
探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口的直径为60cm,灯深40cm,则抛物线的标准方程可能是( )
A、x2=-
| ||
B、y2=
| ||
C、y2=
| ||
D、x2=-
|
函数f(x)=
,则f[f(-2)]=( )
|
| A、2 |
| B、3 |
| C、2log23 |
| D、log27 |
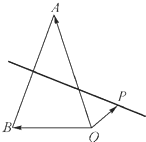 如图,P为△AOB所在平面内一点,向量
如图,P为△AOB所在平面内一点,向量