题目内容
7.若α,β为锐角,$cos(\frac{π}{4}+α)=\frac{1}{3},cos(\frac{π}{4}+\frac{β}{2})=\frac{{\sqrt{3}}}{3}$,则$cos(α-\frac{β}{2})$=( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{6}}}{9}$ | D. | $\frac{{5\sqrt{3}}}{9}$ |
分析 由同角三角函数基本关系可得sin($\frac{π}{4}$+α)和sin($\frac{π}{4}$+$\frac{β}{2}$),整体代入两角差的余弦公式计算可得.
解答 解:α,β为锐角,$cos(\frac{π}{4}+α)=\frac{1}{3},cos(\frac{π}{4}+\frac{β}{2})=\frac{{\sqrt{3}}}{3}$,
∴sin($\frac{π}{4}$+α)=$\sqrt{1-co{s}^{2}(\frac{π}{4}+α)}$=$\frac{2\sqrt{2}}{3}$,
sin($\frac{π}{4}$+$\frac{β}{2}$)=$\sqrt{1-co{s}^{2}(\frac{π}{4}+\frac{β}{2})}$=$\frac{\sqrt{6}}{3}$,
∴$cos(α-\frac{β}{2})$=cos[($\frac{π}{4}$+α)-($\frac{π}{4}$+$\frac{β}{2}$)]
=cos($\frac{π}{4}$+α)cos($\frac{π}{4}$+$\frac{β}{2}$)+sin($\frac{π}{4}$+α)sin($\frac{π}{4}$+$\frac{β}{2}$)
=$\frac{1}{3}×\frac{\sqrt{3}}{3}$+$\frac{2\sqrt{2}}{3}×\frac{\sqrt{6}}{3}$=$\frac{5\sqrt{3}}{9}$.
故选:D.
点评 本题考查两角和与差的余弦公式,涉及同角三角函数基本关系,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.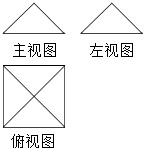 一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )
一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )
 一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )
一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )| A. | 48 | B. | 64 | C. | 80 | D. | 120 |
2.已知$sin(-\frac{3}{2}π+θ)=\frac{1}{5}$,则cosθ=( )
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
16.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若$sinA=\frac{{2\sqrt{2}}}{3}$,a=2,ccosB+bcosC=2acosB,则b的值为( )
| A. | $2\sqrt{6}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{4}$ |
17.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
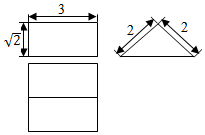

| A. | $\frac{17\sqrt{17}}{6}$π | B. | 34π | C. | 17π | D. | $\frac{17}{4}$π |