题目内容
18.设命题p:|x-2|>1;命题q:x2-(2a+1)x+a(a+1)≤0.若?p是?q的必要不充分条件,求实数a的取值范围.分析 由p:|x-2|>1,解出x的范围.由q:x2-(2a+1)x+a(a+1)≤0,解出x的范围.由于?p是?q的必要不充分条件,可得p是q的充分不必要条件.
解答 解:由p:|x-2|>1,
解得x<1或x>3.…(3分)
由q:x2-(2a+1)x+a(a+1)≤0得(x-a)[x-(a+1)]≥0,
解得x≤a或x≥a+1.…(6分)
∵?p是?q的必要不充分条件,∴p是q的充分不必要条件.…(8分)
∴$\left\{\begin{array}{l}a≥1\\ a+1≤3\end{array}\right.$,则1≤a≤2.
∴实数a的取值范围是[1,2].(10分)
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.已知倾斜角为45°的直线l过抛物线y2=4x的焦点,且与抛物线交于A,B两点,则△OAB(其中O为坐标原点)的面积为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 8 |
7.若α,β为锐角,$cos(\frac{π}{4}+α)=\frac{1}{3},cos(\frac{π}{4}+\frac{β}{2})=\frac{{\sqrt{3}}}{3}$,则$cos(α-\frac{β}{2})$=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{6}}}{9}$ | D. | $\frac{{5\sqrt{3}}}{9}$ |
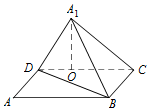 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.