题目内容
已知函数y=f（x）在区间（a，b）内可导，且x0∈（a，b），则
=（ ）
| lim |
| h→∞ |
| f(x0+h)-f(x0-h) |
| h |
| A、f′（x0） |
| B、2f′（x0） |
| C、-2f′（x0） |
| D、0 |
考点：极限及其运算
专题：导数的概念及应用
分析：把要求极限的代数式变形，然后利用导数的概念得答案．
解答：
解：由
=
=
+
=2f′（x0）．
故选：B．
| lim |
| h→0 |
| f(x0+h)-f(x0-h) |
| h |
=
| lim |
| h→0 |
| f(x0+h)-f(x0)+f(x0)-f(x0-h) |
| h |
=
| lim |
| h→0 |
| f(x0+h)-f(x0) |
| h |
| lim |
| h→0 |
| f(x0-h)-f(x0) |
| -h |
=2f′（x0）．
故选：B．
点评：本题考查了极限的求法，考查了导数的概念，是基础题．
练习册系列答案
相关题目
已知定义在R上的函数y=f（x）满足下列三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的0≤x1≤x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）是偶函数；
则下列结论中正确的是（ ）
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的0≤x1≤x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）是偶函数；
则下列结论中正确的是（ ）
| A、f（6.5）＜f（5）＜f（15.5） |
| B、f（5）＜f（6.5）＜f（15.5） |
| C、f（5）＜f（15.5）＜f（6.5） |
| D、f（15.5）＜f（5）＜f（6.5） |
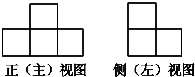用小正方体搭成一个几何体，如图是它的正（主）视图和侧（左）视图，搭成这个几何体的小正方体最多为