题目内容
14.若实数x,y满足x2+y2-2x+2$\sqrt{3}$y+3=0,则x-$\sqrt{3}$y的取值范围是( )| A. | [2,+∞) | B. | (2,6) | C. | [2,6] | D. | [-4,0] |
分析 化圆的一般式方程为标准方程,三角换元由三角函数的值域可得.
解答 解:∵实数x,y满足x2+y2-2x+2$\sqrt{3}$y+3=0,
配方可得(x-1)2+(y+$\sqrt{3}$)2=1,
故可设x-1=cosθ,y+$\sqrt{3}$=sinθ,
则x=1+cosθ,y=-$\sqrt{3}+$sinθ,
∴x-$\sqrt{3}$y=1+cosθ-$\sqrt{3}$(-$\sqrt{3}+$sinθ)
=4+cosθ-$\sqrt{3}$sinθ=4+2cos(θ+$\frac{π}{3}$),
∴当cos(θ+$\frac{π}{3}$)=1时,原式取最大值4+2=6;
当cos(θ+$\frac{π}{3}$)=-1时,原式取最小值4-2=2.
故选:C.
点评 本题考查圆的一般式方程和标准方程,以及三角换元的方法,属中档题.

练习册系列答案
相关题目
4.利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( )
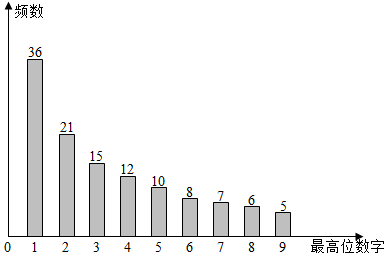

| A. | P=lg(1+$\frac{1}{d}$) | B. | P=$\frac{1}{d+2}$ | C. | P=$\frac{{(d-5)}^{2}}{120}$ | D. | P=$\frac{3}{5}$×$\frac{1}{{2}^{d}}$ |
3.等差数列{an}中,若a1+a9=4,则a5等于( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,