题目内容
19.已知tan$\frac{θ}{2}$=$\frac{1}{2}$,则$\frac{cos(θ-π)sin(π-θ)}{cos(2π-θ)[sin(θ-\frac{π}{2})+1]}$=-2.分析 根据诱导公式将所求的式子化简,根据正切函数的半角公式,求得式子的值.
解答 解:原式=$\frac{-cosθsinθ}{cos(-θ)(-cosθ+1)}$
=$\frac{-sinθcosθ}{cosθ(1-cosθ)}$
=-$\frac{sinθ}{1-cosθ}$
=$-\frac{1}{tan\frac{θ}{2}}$
=-2
故答案为:-2
点评 主要考察利用诱导公式化简及正切函数半角公式.

练习册系列答案
相关题目
14.若实数x,y满足x2+y2-2x+2$\sqrt{3}$y+3=0,则x-$\sqrt{3}$y的取值范围是( )
| A. | [2,+∞) | B. | (2,6) | C. | [2,6] | D. | [-4,0] |
8.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与抛物线y2=4cx(其中c=$\sqrt{{a}^{2}+{b}^{2}}$)交于A,B两点,若|AB|=4c,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{2}$+1 |
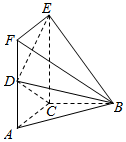 如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.
如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.