题目内容
 在四棱锥P-ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点.
在四棱锥P-ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点.(1)求证:平面PAC⊥平面PCD;
(2)求证:CE∥平面PAB.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由线面垂直得PA⊥CD,由直角性质得CD⊥AC,由此能证明平面PAC⊥平面PCD.
(2)法一:取AD中点M,连EM,CM,则EM∥PA.从而得到EM∥平面PAB.再由MC∥AB,得到MC∥平面PAB,由此证明平面EMC∥平面PAB,从而EC∥平面PAB.
(2)法二:延长DC,AB交于点N,连PN.由已知条件推地出EC∥PN.由此能证明EC∥平面PAB.
(2)法一:取AD中点M,连EM,CM,则EM∥PA.从而得到EM∥平面PAB.再由MC∥AB,得到MC∥平面PAB,由此证明平面EMC∥平面PAB,从而EC∥平面PAB.
(2)法二:延长DC,AB交于点N,连PN.由已知条件推地出EC∥PN.由此能证明EC∥平面PAB.
解答:
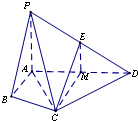 证明:(1)因为PA⊥平面ABCD,CD?平面ABCD,所以PA⊥CD,…(2分)
证明:(1)因为PA⊥平面ABCD,CD?平面ABCD,所以PA⊥CD,…(2分)
又∠ACD=90°,则CD⊥AC,而PA∩AC=A,
所以CD⊥平面PAC,因为CD?平面ACD,…(4分)
所以,平面PAC⊥平面PCD.…(7分)
(2)证法一:取AD中点M,连EM,CM,则EM∥PA.
因为EM?平面PAB,PA?平面PAB,
所以EM∥平面PAB. …(9分)
在Rt△ACD中,AM=CM,所以∠CAD=∠ACM,
又∠BAC=∠CAD,所以∠BAC=∠ACM,
则MC∥AB.
因为MC?平面PAB,AB?平面PAB,
所以MC∥平面PAB.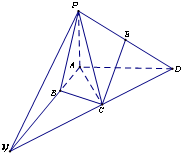 …(12分)
…(12分)
而EM∩MC=M,所以平面EMC∥平面PAB.
由于EC?平面EMC,从而EC∥平面PAB. …(14分)
(2)证法二:延长DC,AB交于点N,连PN.
因为∠NAC=∠DAC,AC⊥CD,
所以C为ND的中点.
而E为PD中点,所以EC∥PN.
因为EC?平面PAB,PN?平面PAB,
所以EC∥平面PAB.…(14分)
 证明:(1)因为PA⊥平面ABCD,CD?平面ABCD,所以PA⊥CD,…(2分)
证明:(1)因为PA⊥平面ABCD,CD?平面ABCD,所以PA⊥CD,…(2分)又∠ACD=90°,则CD⊥AC,而PA∩AC=A,
所以CD⊥平面PAC,因为CD?平面ACD,…(4分)
所以,平面PAC⊥平面PCD.…(7分)
(2)证法一:取AD中点M,连EM,CM,则EM∥PA.
因为EM?平面PAB,PA?平面PAB,
所以EM∥平面PAB. …(9分)
在Rt△ACD中,AM=CM,所以∠CAD=∠ACM,
又∠BAC=∠CAD,所以∠BAC=∠ACM,
则MC∥AB.
因为MC?平面PAB,AB?平面PAB,
所以MC∥平面PAB.
 …(12分)
…(12分)而EM∩MC=M,所以平面EMC∥平面PAB.
由于EC?平面EMC,从而EC∥平面PAB. …(14分)
(2)证法二:延长DC,AB交于点N,连PN.
因为∠NAC=∠DAC,AC⊥CD,
所以C为ND的中点.
而E为PD中点,所以EC∥PN.
因为EC?平面PAB,PN?平面PAB,
所以EC∥平面PAB.…(14分)
点评:本题考查平面与平面垂直的证明,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
的定义域为( )
| 2x-1 |
| lnx |
| A、(0,+∞) |
| B、(0,1)∪(1,+∞) |
| C、(0,1) |
| D、(1,+∞) |
 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A、B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A、B两点,点O为坐标原点.