题目内容
已知直线l经过抛物线x2=4y的焦点，且与抛物线交于A、B两点，点O为坐标原点．（1）证明：
| OA |
| OB |
（2）若△AOB的面积为4，求直线l的方程．
考点：直线与圆锥曲线的关系,平面向量数量积的运算,直线的一般式方程
专题：向量与圆锥曲线,圆锥曲线的定义、性质与方程
分析：（1）由抛物线x2=4y的方程可得焦点F（0，1）．设A（x1，y1），B（x2，y2）．设直线l的方程为：y=kx+1．与抛物线方程联立可得根与系数的关系，再利用数量积
•
=x1x2+y1y2即可证明；
（2）利用（1）及弦长公式、点到直线的距离公式即可得出k．
| OA |
| OB |
（2）利用（1）及弦长公式、点到直线的距离公式即可得出k．
解答：
（1）证明：由抛物线x2=4y的方程可得焦点F（0，1）．
设A（x1，y1），B（x2，y2）．
设直线l的方程为：y=kx+1．
联立
，化为x2-4kx-4=0．
∴x1+x2=4k，x1x2=-4．
∴y1y2=（kx1+1）（kx2+1）=k2x1x2+k（x1+x2）+1=-4k2+4k2+1=1．
∴
•
=x1x2+y1y2=-4+1=-3；
（2）解：由（1）可得|AB|=
=
=4（1+k2）．
点O到直线l的距离d=
．
∴S△OAB=
|AB|d=
×4(1+k2)•
=4，
解得k2=3，
∴k=±
．
∴直线l的方程为：y=±
x+1．
设A（x1，y1），B（x2，y2）．
设直线l的方程为：y=kx+1．
联立
|
∴x1+x2=4k，x1x2=-4．
∴y1y2=（kx1+1）（kx2+1）=k2x1x2+k（x1+x2）+1=-4k2+4k2+1=1．
∴
| OA |
| OB |
（2）解：由（1）可得|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
| (1+k2)[16k2+16] |
点O到直线l的距离d=
| 1 | ||
|
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
解得k2=3，
∴k=±
| 3 |
∴直线l的方程为：y=±
| 3 |
点评：本题考查了直线与抛物线的相交问题转化为方程联立可得根与系数、数量积运算、弦长公式、点到直线的距离公式、三角形的面积计算公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
在函数y=cosx（x∈[-
数列{an}的通项公式为an=4n-1，则bk=
（a1+a2+…+ak）（k∈N*）所确定的数列{bn}的前n项和为（ ）
| 1 |
| k |
| A、n2 |
| B、n（n+1） |
| C、n（n+2） |
| D、n（2n+1） |
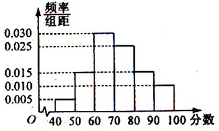我校从高一年级学生中随机抽取部分学生，将他们的数学竞赛成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以统计，得到如图所示的频率分布直方图．
在四棱锥P-ABCD中，∠ACD=90°，∠BAC=∠CAD，PA⊥平面ABCD，E为PD的中点．