题目内容

5．集合P={y|y=-x2+2}，Q={x|y=-x+2}则P∩Q是（　　）
A．（0，2），（1，1）B．{（0，2），（1，1）}C．∅D．{y|y≤2}

分析 先分别求出集合P，Q，由此利用交集定义能求出P∩Q．

解答 解：∵集合P={y|y=-x2+2}={y|y≤2}，
Q={x|y=-x+2}=R，
∴P∩Q={y|y≤2}．
故选：D．

点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．

练习册系列答案
相关题目
15．已知A（-1，0），B是圆F：x2-2x+y2-11=0（F为圆心）上一动点，线段AB的垂直平分线交BF于P，则动点P的轨迹方程为（　　）
A．$\frac{x^2}{12}+\frac{y^2}{11}=1$B．$\frac{x^2}{36}-\frac{y^2}{35}=1$C．$\frac{x^2}{3}-\frac{y^2}{2}=1$D．$\frac{x^2}{3}+\frac{y^2}{2}=1$
16．要排出某班一天中语文、数学、政治、英语、体育、艺术六堂课的课程表，要求数学排在上午（前4节），体育排在下午（后2节），不同排法总数是（　　）
A．720B．120C．144D．192
13．（Ⅰ）已知在△ABC中，AB=1，BC=2，∠B=$\frac{π}{3}$，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$求（2$\overrightarrow{a}$-3$\overrightarrow{b}$）•（4$\overrightarrow{a}$+$\overrightarrow{b}$）；
（Ⅱ）已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-1，3），且向量t$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow{a}$-$\overrightarrow{b}$平行，求t的值．
20．如图为一个简单组合体的三视图，其中正视图由 一个半圆和一个正方形组成，则该组合体的表面积为（　　）
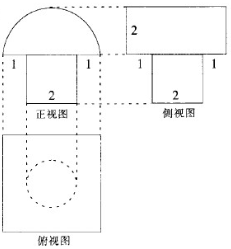
A．20+17πB．20+16πC．16+17πD．16+l6π
10．已知集合A={-2，-1，0，1，2}，B={x|lgx≤0}，则A∩B=（　　）
A．{1}B．{0，1}C．{0，1，2}D．{1，2}
17．已知D=$\left\{{\left.{（{x，y}）}\right|\left\{\begin{array}{l}x+y-2≤0\\ x-y+2≤0\\ 3x-y+6≥0\end{array}\right.}\right\}$，给出下列四个命题：
P1：?（x，y）∈D，x+y+1≥0；
P2：?（x，y）∈D，2x-y+2≤0；
P3：?（x，y）∈D，$\frac{y+1}{x-1}$≤-4；
P4：?（x，y）∈D，x2+y2≤2．
其中真命题的是（　　）
A．P1，P2B．P2，P3C．P2，P4D．P3，P4
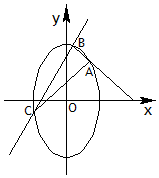14．如图，点$A（1，\sqrt{3}）$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点，过点A引两直线与椭圆分别交于B，C两点．
（1）求椭圆方程；
（2）若直线AB，AC与x轴围成以点A为顶点的等腰三角形，求△ABC的面积最大值，并求出此时直线BC的方程．
15．sin（-1740°）的值是（　　）
A．-$\frac{\sqrt{3}}{2}$B．-$\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网