题目内容
17.已知D=$\left\{{\left.{({x,y})}\right|\left\{\begin{array}{l}x+y-2≤0\\ x-y+2≤0\\ 3x-y+6≥0\end{array}\right.}\right\}$,给出下列四个命题:P1:?(x,y)∈D,x+y+1≥0;
P2:?(x,y)∈D,2x-y+2≤0;
P3:?(x,y)∈D,$\frac{y+1}{x-1}$≤-4;
P4:?(x,y)∈D,x2+y2≤2.
其中真命题的是( )
| A. | P1,P2 | B. | P2,P3 | C. | P2,P4 | D. | P3,P4 |
分析 画出约束条件不是的可行域,利用目标函数的几何意义,求出范围,判断选项的正误即可.
解答 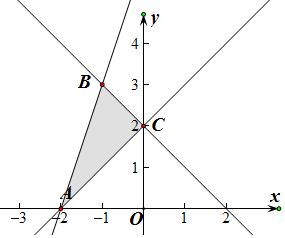 解:不等式组$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≤0}\\{3x-y+6≥0}\end{array}\right.$的可行域如图,
解:不等式组$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≤0}\\{3x-y+6≥0}\end{array}\right.$的可行域如图,
p1:A(-2,0)点,-2+0+1=-1,
故?(x,y)∈D,x+y≥0为假命题;
p2:A(-1,3)点,-2-3+2=-3,
故?(x,y)∈D,2x-y+2≤0为真命题;
p3:C(0,2)点,$\frac{2+1}{0-1}$=-3,
故?(x,y)∈D,$\frac{y+1}{x-1}$≤-4为假命题;
p4:(-1,1)点,x2+y2=2
故?(x,y)∈D,x2+y2≤2为真命题.
可得选项p2,p4正确.
故选:C.
点评 本题考查线性规划的解得应用,命题的真假的判断,正确画出可行域以及目标函数的几何意义是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
7.已知函数f(x)=2|x|,记a=f(log0.53),b=log25,c=f(0),则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
5.集合P={y|y=-x2+2},Q={x|y=-x+2}则P∩Q是( )
| A. | (0,2),(1,1) | B. | {(0,2),(1,1)} | C. | ∅ | D. | {y|y≤2} |
2.已知i是虚数单位,(1+2i)z1=-1+3i,${z_2}=1+{({1+i})^{10}}$,z1、z2在复平面上对应的点分别为A、B,则|AB|=( )
| A. | 31 | B. | 33 | C. | $\sqrt{31}$ | D. | $\sqrt{33}$ |
9.已知命题p:存在向量$\overrightarrow{a}$,$\overrightarrow{b}$,使得$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,命题q:对任意的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$.则下列判断正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
7.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为( )


| A. | $\frac{28}{3}$ | B. | $\frac{{28\sqrt{2}}}{3}$ | C. | 28 | D. | $22+6\sqrt{3}$ |