题目内容
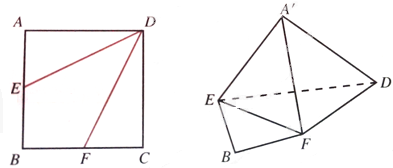
 一个四棱锥S-ABCD的底面是边长为a的正方形,侧面展开图如图所示.SC为四棱锥中最长的侧棱,点E为AB的中点
一个四棱锥S-ABCD的底面是边长为a的正方形,侧面展开图如图所示.SC为四棱锥中最长的侧棱,点E为AB的中点(1)画出四棱锥S-ABCD的示意图,求二面角E-SC-D的大小;
(2)求点D到平面SEC的距离.
考点:点、线、面间的距离计算,二面角的平面角及求法
专题:空间位置关系与距离
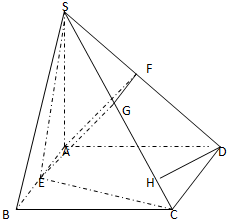
分析:(1)作出四棱锥S-ABCD的示意图,分别取SC、SD的中点G、F,连GE、GF、FA,由已知条件推导出面SEC⊥面SCD,由此得到二面角E-SC-D的大小为90°.
(2)作DH⊥SC于H,则DH之长即为点D到面SEC的距离,由此能求出点D到面SEC的距离.
(2)作DH⊥SC于H,则DH之长即为点D到面SEC的距离,由此能求出点D到面SEC的距离.
解答:
 (12分)
(12分)
解:(1)四棱锥S-ABCD的示意图如图所示,…(2分)
分别取SC、SD的中点G、F,连GE、GF、FA,
则GF∥EA,GF=EA,∴AF∥EG,
∵SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,
∴SA⊥底面ABCD,SA⊥CD,
又∵AD⊥CD,∴CD⊥面SAD,∴CD⊥AF,
又∵SA=AD,F是中点,∴AF⊥SD,
∴AF⊥面SCD,EG⊥面SCD,∴面SEC⊥面SCD,
∴二面角E-SC-D的大小为90°.…(8分)
(2)作DH⊥SC于H,
∵面SEC⊥面SCD,∴DH⊥面SEC,
∴DH之长即为点D到面SEC的距离,
∵在Rt△SCD中,DH=
=
=
a,
答:点D到面SEC的距离为
a.…(12分)
 (12分)
(12分)解:(1)四棱锥S-ABCD的示意图如图所示,…(2分)
分别取SC、SD的中点G、F,连GE、GF、FA,
则GF∥EA,GF=EA,∴AF∥EG,
∵SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,
∴SA⊥底面ABCD,SA⊥CD,
又∵AD⊥CD,∴CD⊥面SAD,∴CD⊥AF,
又∵SA=AD,F是中点,∴AF⊥SD,
∴AF⊥面SCD,EG⊥面SCD,∴面SEC⊥面SCD,
∴二面角E-SC-D的大小为90°.…(8分)
(2)作DH⊥SC于H,
∵面SEC⊥面SCD,∴DH⊥面SEC,
∴DH之长即为点D到面SEC的距离,
∵在Rt△SCD中,DH=
| SD•DC |
| SC |
| ||
|
| ||
| 3 |
答:点D到面SEC的距离为
| ||
| 3 |
点评:本题考查二面角大小的求法,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
(x2-x+1)10展开式中x3项的系数为( )
| A、-210 | B、210 |
| C、30 | D、-30 |
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则动点P到点C的距离小于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
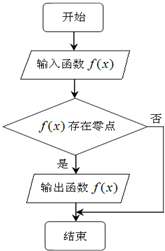 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|,则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|,则输出的函数的个数为( )