题目内容
15.已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=11,则线段AB的中点到y轴的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
分析 求得抛物线的焦点坐标,根据抛物线的焦点弦公式,求得x1+x2=10,则线段AB的中点横坐标为$\frac{{x}_{1}+{x}_{2}}{2}$,即可求得线段AB的中点到y轴的距离.
解答 解:∵F是抛物线y2=2x的焦点F($\frac{1}{2}$,0),准线方程x=-$\frac{1}{2}$,
设A(x1,y1),B(x2,y2)
∴|AF|+|BF|=x1+$\frac{1}{2}$+x2+$\frac{1}{2}$=11
∴x1+x2=10,
∴线段AB的中点横坐标为$\frac{{x}_{1}+{x}_{2}}{2}$=5,
∴线段AB的中点到y轴的距离为5,
故选:C.
点评 本题考查解决抛物线上的点到焦点的距离问题,利用抛物线的定义将到焦点的距离转化为到准线的距离是解题的关键,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
20.已知$\overline{z}$为复数z的共轭复数,且(1-i)z=1+i,则$\overline{z}$为( )
| A. | -i | B. | i | C. | 1-i | D. | 1+i |
4.已知λ∈R,向量$\overrightarrow{a}$=( 3,λ ),$\overrightarrow{b}$=(λ-1,2),则“λ=$\frac{3}{5}$”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.函数f(x)=2|sinx|的最小正周期为( )
| A. | 2π | B. | $\frac{3π}{2}$ | C. | π | D. | $\frac{π}{2}$ |
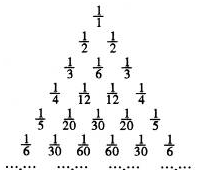 德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.
德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.