题目内容
已知等差数列{an}的前n项和为Sn,首项为1的等比数列{bn}的公比为q,S2=a3=b3,且a1,a3,b2成等比数列.
(1)求{an}和{bn}的通项公式;
(2)设数列{bn}的前n项和为Tn,若2Sn-nan=b+loga(2Tn+1)对一切正整数n成立,求实数a,b的值.
(1)求{an}和{bn}的通项公式;
(2)设数列{bn}的前n项和为Tn,若2Sn-nan=b+loga(2Tn+1)对一切正整数n成立,求实数a,b的值.
考点:等差数列与等比数列的综合,等差数列的前n项和,等比数列的前n项和
专题:计算题
分析:(1)设等差数列{an}的公差为d,由S2=a3,得2a1+d=a1+2d,故有a1=d.由a3=b3,得a1+2d=b1q2,故有3a1=q2.由a1,a3,b4成等差数列,得a32=a1•b4,故有9a1=q3.由此能求出{an}和{bn}的通项公式.
(2)由2Sn-nan=2×[3n+
×3]-n•3n=3n,2Tn+1=2×
+1=3n,知若2Sn-nan=b+loga(2Tn+1)对一切正整数n成立,则3n=b+nloga3,由此能求出实数a,b的值.
(2)由2Sn-nan=2×[3n+
| n(n-1) |
| 2 |
| 1×(1-3n) |
| 1-3 |
解答:
解:(1)设等差数列{an}的公差为d,
由S2=a3,得2a1+d=a1+2d,故有a1=d.
由a3=b3,得a1+2d=b1q2,故有3a1=q2.①
由a1,a3,b4成等差数列,得a32=a1•b4,故有9a1=q3.②
由①②解得a1=3,q=3,
∴an=3+(n-1)•3=3n,bn=3n-1.
(2)∵2Sn-nan=2×[3n+
×3]-n•3n=3n,
2Tn+1=2×
+1=3n,
若2Sn-nan=b+loga(2Tn+1)对一切正整数n成立,
则3n=b+nloga3,
∴
,解得a=
,b=0.
由S2=a3,得2a1+d=a1+2d,故有a1=d.
由a3=b3,得a1+2d=b1q2,故有3a1=q2.①
由a1,a3,b4成等差数列,得a32=a1•b4,故有9a1=q3.②
由①②解得a1=3,q=3,
∴an=3+(n-1)•3=3n,bn=3n-1.
(2)∵2Sn-nan=2×[3n+
| n(n-1) |
| 2 |
2Tn+1=2×
| 1×(1-3n) |
| 1-3 |
若2Sn-nan=b+loga(2Tn+1)对一切正整数n成立,
则3n=b+nloga3,
∴
|
| 3 | 3 |
点评:本题考查等差数列和等比数列的性质和应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,尤其是恒成立问题的转化.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
下表是X的分布列,则a=( )
| X | 1 | 2 | 3 |
| P | 0.5 | a | 0.3 |
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
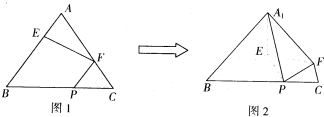 如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设
如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设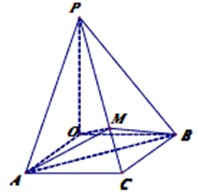 如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
 设图中的正方体的棱长为a(1)图中哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小.(3)求异面直线BC和AA1的距离.
设图中的正方体的棱长为a(1)图中哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小.(3)求异面直线BC和AA1的距离.