题目内容
16.在△ABC中,AB=3,AC=2,∠BAC=60°,点P是△ABC内一点(含边界),若$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$,则|$\overrightarrow{AP}$|的取值范围为( )| A. | [2,$\frac{2\sqrt{10+3\sqrt{3}}}{3}$] | B. | [2,$\frac{8}{3}$] | C. | [0,$\frac{2\sqrt{13}}{3}$] | D. | [2,$\frac{2\sqrt{13}}{3}$] |
分析 在AB上取一点D,使得$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AB}$.过D,作DH∥AC,交AC于H,可得点P在线段DH上,当P在D处时,|$\overrightarrow{AP}$|最小为$\frac{2}{3}AB=2$;当P在H处时,|$\overrightarrow{AP}$|最大,∵$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$,且B,P,C共线,⇒${\overrightarrow{AP}}^{2}=\frac{1}{9}{\overrightarrow{AC}}^{2}+\frac{4}{9}\overrightarrow{A{B}^{2}}+\frac{4}{9}\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{52}{9}$,即可得|$\overrightarrow{AP}$|的取值范围.
解答  解:在AB上取一点D,使得$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AB}$.过D,作DH∥AC,交AC于H,
解:在AB上取一点D,使得$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AB}$.过D,作DH∥AC,交AC于H,
∵$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$,且点P是△ABC内一点(含边界),∵点P在线段DH上
当P在D处时,|$\overrightarrow{AP}$|最小为$\frac{2}{3}AB=2$,
当P在H处时,|$\overrightarrow{AP}$|最大,∵$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$,且B,P,C共线,∴$λ=\frac{1}{3}$
∴$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AB}$,⇒${\overrightarrow{AP}}^{2}=\frac{1}{9}{\overrightarrow{AC}}^{2}+\frac{4}{9}\overrightarrow{A{B}^{2}}+\frac{4}{9}\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{52}{9}$
则|$\overrightarrow{AP}$|的取值范围为[2,$\frac{2\sqrt{13}}{2}$].
故选:D.
点评 本题考查了向量的线性运算,向量的模运算,考查了转化思想,属于中档题.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案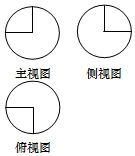 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是$\frac{28π}{3}$,则三视图中圆的半径为( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是$\frac{28π}{3}$,则三视图中圆的半径为( )