题目内容

若
OA
=
a
，
OB
=
b
，则∠AOB平分线上的向量
OM
=（　　）
A．
a
|
a
|
+
b
|
b
|
B．λ(
a
|
a
|
+
b
|
b
|
)，λ由
OM
确定
C．
a
+
b
|
a
+
b
|
D．
|
b
|
a
+|
a
|
b
|
a
|+|
b
|
∵
OA
=
a
，
OB
=
b

∴
OA
|
OA
|
=
a
|
a
|
，
OB
|
OB
|
=
b
|
b
|

∴以
OA
|
OA
|
，
OB
|
OB
|
为邻边做平行四边形OACB也为菱形
∴OC平分∠AOB
∴根据向量加法的平行四边形法则
可得
OC
=
OA
|
OA
|
+
OB
|
OB
|

∵
OM
与
OC
共线
∴由共线定理可得存在唯一的实数λ使得
OM
=λ
OC
=λ（
a
|
a
|
+
b
|
b
|
）（λ由
OM
确定）
故答案选B
练习册系列答案
相关题目
已知O为△ABC的外心，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
（1）若
OA
=
a
，
OB
=
b
，
OC
=
c
，
OH
=
h
，试用
a
、
b
、
c
表示
h
；
（2）证明：
AH
⊥
BC
；
（3）若△ABC的∠A=60°，∠B=45°，外接圆的半径为R，用R表示|
h
|．
已知O是线段AB外一点，若
OA
=
a
，
OB
=
b
．
（1）设点A1、A2是线段AB的三等分点，△OAA1、△OA1A2及△OA2B的重心依次为G1、G2、G3，试用向量
a
、
b
表示
OG1
+
OG2
+
OG3
；
（2）如果在线段AB上有若干个等分点，你能得到什么结论？请证明你的结论．
若
OA
=
a
，
OB
=
b
，则∠AOB平分线上的向量
OM
=（　　）
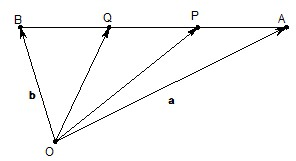（1）如图，设点P，Q是线段AB的三等分点，若
OA
=
a
，
OB
=
b
，试用
a
，
b
表示
OP
，
OQ
，并判断
OP
+
OQ
与
OA
+
OB
的关系；
（2）受（1）的启示，如果点A1，A2，A3，…，An-1是AB的n（n≥3）等分点，你能得到什么结论？请证明你的结论．
在△OAB中，C是AB边上一点，且
BC
CA
=λ（λ＞0），若
OA
=
a
，
OB
=
b
，用
a
、
b
表示
OC
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网