题目内容
1.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒,若一名行人来到该路口遇到红灯,则等待的时间不超过15秒就出现绿灯的概率为( )| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
分析 求出一名行人前25秒来到该路口遇到红灯,即可求出至少需要等待15秒才出现绿灯的概率,从而求出等待的时间不超过15秒就出现绿灯的概率.
解答 解:∵红灯持续时间为40秒,至少需要等待15秒才出现绿灯,
∴一名行人前25秒来到该路口遇到红灯,
∴至少需要等待15秒才出现绿灯的概率为 $\frac{25}{40}$=$\frac{5}{8}$,
故等待的时间不超过15秒就出现绿灯的概率p=1-$\frac{5}{8}$=$\frac{3}{8}$,
故选:C.
点评 本题考查概率的计算,考查几何概型,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16. 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A(B)、C、D、O为顶点的四面体的外接球表面积为( )
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A(B)、C、D、O为顶点的四面体的外接球表面积为( )
 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A(B)、C、D、O为顶点的四面体的外接球表面积为( )
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A(B)、C、D、O为顶点的四面体的外接球表面积为( )| A. | 20π | B. | 24π | C. | 16π | D. | 18π |
6.已知函数f(x)=ex+ln(x+1)的图象在(0,f(0))处的切线与直线x-ny+4=0垂直,则n的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
10.在数列{an}中,若存在非零实数T,使得${a_{n+T}}={a_n}({N∈{n^*}})$成立,则称数列{an}是以T为周期的周期数列.若数列{bn}满足bn+1=|bn-bn-1|,且b1=1,b2=a(a≠0),则当数列{bn}的周期最小时,其前2017项的和为( )
| A. | 672 | B. | 673 | C. | 1345 | D. | 3025 |
11.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,若|AB|=4,则C的实轴长为( )
| A. | 4 | B. | 2 | C. | 4$\sqrt{3}$ | D. | 8 |
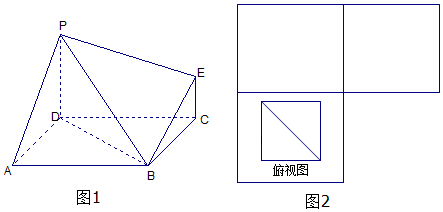
 如图,在三棱锥A-BCD中,E是AC中点,F在AD上,且2AF=FD,若三棱锥A-BEF的体积是1,则四棱锥B-ECDF的体积为5.
如图,在三棱锥A-BCD中,E是AC中点,F在AD上,且2AF=FD,若三棱锥A-BEF的体积是1,则四棱锥B-ECDF的体积为5.