题目内容
11.图1为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.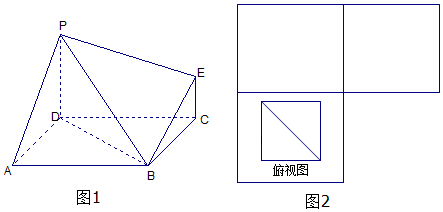
(1)图2方框内已给出了该几何体的俯视图,请在方框内画出该几何体的正(主)视图和侧(左)视图;
(2)求证:BE∥平面PDA.
(3)求四棱锥B-CEPD的体积.
分析 (1)由题设条件能作出该组合体的主视图和侧视图.
(2)推导出EC∥平面PDA,BC∥平面PDA,从而平面BEC∥平面PDA,由此能证明BE∥平面PDA.
(3)推导出平面PDCE⊥平面ABCD,从而BC⊥平面PDCE,由此能求出四棱锥B-CEPD的体积.
解答 解:(1)该组合体的主视图和侧视图如右图示:-----(2分)
证明:(2)∵EC∥PD,PD?平面PDA,EC?平面PDA,
∴EC∥平面PDA,(3分)
同理可得BC∥平面PDA,(4分)
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,
∴平面BEC∥平面PDA,(6分)
又∵BE?平面EBC,∴BE∥平面PDA.(7分)
解:(3)∵PD⊥平面ABCD,PD?平面PDCE,
∴平面PDCE⊥平面ABCD,
∵BC⊥CD,又平面ABCD∩平面PDCE=CD,BC?平面ABCD,
∴BC⊥平面PDCE,(10分)
∵S梯形PDCE=$\frac{1}{2}(PD+EC)•DC=\frac{1}{2}×3×2$=3,(11分)
∴四棱锥B-CEPD的体积${V}_{B-CEPD}=\frac{1}{3}{S}_{梯形PDCE}•BC=\frac{1}{3}×3×2$=2.(12分)
点评 本题三视图的作法,考查线面平行的证明,考查四棱锥的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想、方程思想、整体思想,是中档题.

练习册系列答案
相关题目
4.如果命题“¬(p∨q)”为假命题,则( )
| A. | p,q均为真命题 | B. | p,q中至少有一个为真命题 | ||
| C. | p,q均为假命题 | D. | p,q中至多有一个为真命题 |
6.等差数列{an}的公差为d,an>0,前n项和为Sn,若a2,S3,a2+S5成等比数列,则$\frac{d}{a_1}$=( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
16.曲线y=xlnx在x=e处的切线方程为( )
| A. | y=x-e | B. | y=2x-e | C. | y=x | D. | y=x+1 |
1.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒,若一名行人来到该路口遇到红灯,则等待的时间不超过15秒就出现绿灯的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
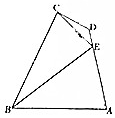 如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$
如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$