题目内容
12.在等比数列{an}中,公比q≠1,等差数列{bn}满足b1=a1=3,b4=a2,b13=a3(I)求数列{an}与{bn}的通项公式;
(II)记cn=(-1)nbn+an,求数列{cn}的前2n项和S2n.
分析 (Ⅰ)设等比数列{an}的公比为q(q≠1),等差数列{bn}的公差为d,根据b1=a1,b4=a2,b13=a3及等差、等比数列的通项公式列关于q,d的方程组解出即得q,d,再代入通项公式即可;
(Ⅱ)根据题意,由(Ⅰ)可得cn=(-1)n(2n+1)+3n,利用分组求和法分析可得S2n=(3+32+33+…+32n)+[(-3)+5+(-7)+9+…-(4n-1)+(4n+1)],分组计算即可得答案.
解答 解:(Ⅰ)根据题意,设等比数列{an}的公比为q(q≠1),等差数列{bn}的公差为d.
由已知得:a2=3q,a3=3q2,b1=3,b4=3+3d,b13=3+12d,
则有$\left\{\begin{array}{l}{3+3d=3q}\\{3+12d=3{q}^{2}}\end{array}\right.$,解可得q=3或 q=1(舍去),
此时d=2,
所以an=3n,bn=2n+1;
(Ⅱ)根据题意,记cn=(-1)nbn+an,则cn=(-1)n(2n+1)+3n,
则S2n=(3+32+33+…+32n)+[(-3)+5+(-7)+9+…-(4n-1)+(4n+1)]
=$\frac{3(1-{3}^{2n})}{1-3}$+[(5-3)+(9-7)+…+(4n+1)-(4n-1)]
=$\frac{{3}^{2n+1}-3}{2}$+2n.
点评 本题考查等差、等比数列通项以及数列的分组求和法,关键是求出数列{an}与{bn}的通项公式.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
4.如果命题“¬(p∨q)”为假命题,则( )
| A. | p,q均为真命题 | B. | p,q中至少有一个为真命题 | ||
| C. | p,q均为假命题 | D. | p,q中至多有一个为真命题 |
1.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒,若一名行人来到该路口遇到红灯,则等待的时间不超过15秒就出现绿灯的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
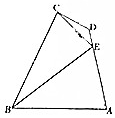 如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$
如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$