题目内容
11.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,若|AB|=4,则C的实轴长为( )| A. | 4 | B. | 2 | C. | 4$\sqrt{3}$ | D. | 8 |
分析 根据题意,设出双曲线方程,由抛物线的几何性质可得抛物线y2=16x的准线方程,则可以设出A、B的坐标,利用|AB|=4,可得A、B的坐标,将其坐标代入双曲线方程可得λ的值,将其变形可得双曲线的标准方程,由实轴的公式计算可得答案.
解答 解:根据题意,要求等轴双曲线C的中心在原点,焦点在x轴上,
则可以设其方程为:x2-y2=λ,(λ>0)
对于抛物线y2=16x,其准线方程为x=-4,
设等轴双曲线与抛物线的准线x=-4的两个交点A(-4,y),B(-4,-y)(y>0),
若|AB|=4,则有|y-(-y)|=4,解可得y=2,
即A(-4,2),B(-4,-2),
代入双曲线方程可得:16-4=λ,解可得λ=12,
则该双曲线的标准方程为:$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{12}$=1,
则a=$\sqrt{12}$=2$\sqrt{3}$,其C的实轴长2a=4$\sqrt{3}$;
故选:C.
点评 本题考查抛物线,双曲线的几何性质,关键是依据题意设出等轴双曲线的方程.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
1.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒,若一名行人来到该路口遇到红灯,则等待的时间不超过15秒就出现绿灯的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
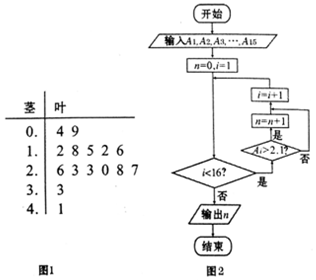 图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.
图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.



 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.