题目内容
6.设函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),x<1}\\{-{2}^{x-1},x≥1}\end{array}\right.$,则f(f(log212))=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先求出f(log212),再求出f(f(log212))即可.
解答 解:∵f(log212)=-6,
∴f(-6)=1+3=4,
故选:D.
点评 本题考查分段函数的求值,主要考查对数的运算性质,属于基础题.

练习册系列答案
相关题目
15.在△ABC中,a,b,c分别为内角A,B,C的对边,3cosA-cos(B+C)=1,a=$\sqrt{15}$,B=$\frac{π}{4}$,则b等于( )
| A. | $\sqrt{10}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
16.在四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD为正方形,E为PC的中点.若异面直线PA与BE所成的角为45°,则四棱锥的体积是( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
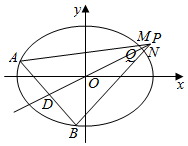 如图,已知直线OP交椭圆C:$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1于点Q,其中O为坐标原点,点P的坐标为(2,1),$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$,若椭圆C不经过原点的弦AB被直线OP平分于点D,且直线AP,BP与椭圆C的另一交点分别为M,N.
如图,已知直线OP交椭圆C:$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1于点Q,其中O为坐标原点,点P的坐标为(2,1),$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$,若椭圆C不经过原点的弦AB被直线OP平分于点D,且直线AP,BP与椭圆C的另一交点分别为M,N.