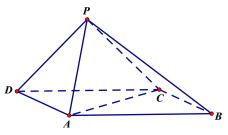
题目内容
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求异面直线AB与PD所成角的余弦值;
(Ⅱ)证明:平面![]() 平面PBD;
平面PBD;
(Ⅲ)求直线DC与平面PBD所成角的正弦值.

【答案】(Ⅰ)![]() (Ⅱ)详见解析(Ⅲ)
(Ⅱ)详见解析(Ⅲ)![]()
【解析】
(Ⅰ)由![]() ,得
,得![]() 是异面直线AB与PD所成角
是异面直线AB与PD所成角![]() 或所成角的补角
或所成角的补角![]() ,利用余弦定理能求出异面直线AB与PD所成角的余弦值;(Ⅱ)由勾股定理得
,利用余弦定理能求出异面直线AB与PD所成角的余弦值;(Ⅱ)由勾股定理得![]() ,再由
,再由![]() ,得
,得![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面PBD;
平面PBD;
(Ⅲ)由![]() ,得直线DC与平面PBD所成角即为AB与平面PBD所成角,过点A作
,得直线DC与平面PBD所成角即为AB与平面PBD所成角,过点A作![]() ,交PD于点H,连结BH,推导出
,交PD于点H,连结BH,推导出![]() 是直线AB与平面PBD所成角,由此能求出直线DC与平面PBD所成角的正弦值。
是直线AB与平面PBD所成角,由此能求出直线DC与平面PBD所成角的正弦值。
解:(Ⅰ)![]() ,
,

![]() 是异面直线AB与PD所成角
是异面直线AB与PD所成角![]() 或所成角的补角
或所成角的补角![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]()
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() 为正方形,
为正方形,![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,![]() 中,
中,![]() ,
,
![]() .
.
![]() 异面直线AB与PD所成角的余弦值为
异面直线AB与PD所成角的余弦值为![]() .
.
(Ⅱ)证明:![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
又![]() ,
,![]() ,
,![]() 平面PAD,
平面PAD,
又![]() 平面PBD,
平面PBD,![]() 平面
平面![]() 平面PBD.
平面PBD.
(Ⅲ)![]() ,
,![]() 直线DC与平面PBD所成角即为AB与平面PBD所成角,
直线DC与平面PBD所成角即为AB与平面PBD所成角,
![]() 过点A作
过点A作![]() ,交PD于点H,连结BH,
,交PD于点H,连结BH,
由(Ⅱ)知平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 为斜线AB在平面PBD内的射影,
为斜线AB在平面PBD内的射影,
![]() 是直线AB与平面PBD所成角,
是直线AB与平面PBD所成角,
![]() 中,
中,![]() ,故
,故![]() 中,
中,![]() ,
,
![]() 直线DC与平面PBD所成角的正弦值为
直线DC与平面PBD所成角的正弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目