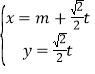题目内容
【题目】在平面直角坐标系中，曲线
与坐标轴的交点都在圆C上.
（1）求圆C的方程；
（2）若圆C与直线
交于A，B两点，且
，求a的值.
【答案】（1）
（2）
【解析】
（1）求出曲线
与坐标轴的三个交点，根据这三个交点在圆上可求出圆心坐标和半径，从而可得圆的方程；
（2）设A
，B
，联立直线与圆的方程，根据根与系数的关系可得
，
，根据
得
，化为
，进而可解得
.
（1）曲线与坐标轴的交点为(0，1)，(
,0)，
由题意可设圆C的圆心坐标为(3，
)，
∴
，解得
，
∴圆C的半径为
，
∴圆C的方程为.
（2）设点A、B的坐标分别为A，B，其坐标满足方程组
，消去
得到方程
，
由已知得，判别式
①，
由根与系数的关系得，②，
由得.
又∵
，
，∴可化为③，
将②代入③解得，经检验，满足①，即
，
∴.
练习册系列答案
相关题目
【题目】高中生在被问及“家，朋友聚集的地方，个人空间”三个场所中“感到最幸福的场所在哪里？”这个问题时，从中国某城市的高中生中，随机抽取了55人，从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是：选择家的占
、朋友聚集的地方占
、个人空间占.美国高中生答题情况是：朋友聚集的地方占
、家占
、个人空间占.如下表：
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
（Ⅰ）请将
列联表补充完整；试判断能否有
的把握认为“恋家”与否与国别有关；
（Ⅱ）从被调查的不“恋家”的美国学生中，用分层抽样的方法选出4人接受进一步调查，再从4人中随机抽取2人到中国交流学习，求2人中含有在“个人空间”感到幸福的学生的概率.
附：
，其中
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
