题目内容
若函数f（x）=（x+1）（x2+ax+b），（a，b∈R）的图象关于点（2，0）对称，且对任意实数x≥m时，f（x）≥0恒成立，则实数m的最小值为 ．
考点：函数恒成立问题
专题：综合题,导数的综合应用
分析：取f（x）图象上的两点（0，b），（-1，0），易求两对称点，代入解析式可得方程组，解出a，b可得函数解析式，利用导数可判断函数的单调性，再由函数零点可知f（x）的符号变化情况，进而可得m范围．
解答：
解：取f（x）图象上的两点（0，b），（-1，0），
其关于（2，0）的对称的分别为（4，-b），（5，0），
则
，解得
，
∴f（x）=（x+1）（x2-7x+10），
f′（x）=x2-7x+10+（x+1）（2x-7）=3[x-（2+
）][x-（2-
）]，
则x＜2-
或x＞2+
时，f′（x）＞0，当2-
＜x＜2+
时，f′（x）＜0，
∴f（x）在（-∞，2-
]，[2+
，+∞）上递增；在（2-
，2+
）上递减．
又f（x）=（x+1）（x-2）（x-5），
∴f（5）=0，即x≥5时，f（x）≥0，
∵对任意实数x≥m时，f（x）≥0恒成立，
∴m≥5，
∴实数m的最小值为5，
故答案为：5．
其关于（2，0）的对称的分别为（4，-b），（5，0），
则
|
|
∴f（x）=（x+1）（x2-7x+10），
f′（x）=x2-7x+10+（x+1）（2x-7）=3[x-（2+
| 3 |
| 3 |
则x＜2-
| 3 |
| 3 |
| 3 |
| 3 |
∴f（x）在（-∞，2-
| 3 |
| 3 |
| 3 |
| 3 |
又f（x）=（x+1）（x-2）（x-5），
∴f（5）=0，即x≥5时，f（x）≥0，
∵对任意实数x≥m时，f（x）≥0恒成立，
∴m≥5，
∴实数m的最小值为5，
故答案为：5．
点评：该题考查函数恒成立问题，考查利用导数研究函数的单调性，考查学生综合运用知识解决问题的能力．
练习册系列答案
相关题目
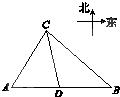如图，港口A北偏东30°方向的C处有一检查站，港口正东方向的B处有一轮船，距离检查站7海里，该轮船从B处沿正西方向航行3海里后到达D处观测站，已知观测站与检查站距离5海里，则此时轮船离港口A有