题目内容
1.对任意实数x>1,y>$\frac{1}{2}$,不等式p≤$\frac{{x}^{2}}{2y-1}$+$\frac{4{y}^{2}}{x-1}$恒成立,则实数p的最大值为8.分析 根据不等式p≤$\frac{{x}^{2}}{2y-1}$+$\frac{4{y}^{2}}{x-1}$恒成立,转化为求$\frac{{x}^{2}}{2y-1}$+$\frac{4{y}^{2}}{x-1}$的最小值即可,利用换元法,结合基本不等式进行求解即可.
解答 解:设a=2y-1,b=x-1,
∵x>1,y>$\frac{1}{2}$,
∴a>0,b>0,且x=b+1,y=$\frac{1}{2}$(a+1),
则$\frac{{x}^{2}}{2y-1}$+$\frac{4{y}^{2}}{x-1}$=$\frac{(b+1)^{2}}{a}$+$\frac{(a+1)^{2}}{b}$≥2×$\frac{(a+1)(b+1)}{\sqrt{ab}}$=2×$\frac{ab+(a+b)+1}{\sqrt{ab}}$=2($\sqrt{ab}$+$\frac{1}{\sqrt{ab}}$+$\frac{a+b}{\sqrt{ab}}$)≥2×(2$\sqrt{\sqrt{ab}•\frac{1}{\sqrt{ab}}}$+$\frac{2\sqrt{ab}}{\sqrt{ab}}$)=2(2+2)=8,
当且仅当a=b=1,即x=2,y=1时,取等号.
∴p≤8,
即p的最大值为8,
故答案为:8.
点评 本题主要考查不等式恒成立问题,利用换元法转化求函数的最小值,多次使用基本不等式是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
6.某四面体的三视图如图所示,该四面体外接球的表面积为( )
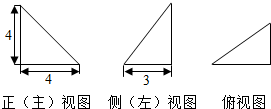

| A. | 41π | B. | $\frac{41π}{2}$ | C. | 48π | D. | 24π |