Question

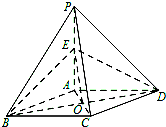
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，且PA⊥底面ABCD，BD⊥PC，E是PA的中点．
（Ⅰ）求证：平面PAC⊥平面EBD；
（Ⅱ）若PA=AB=AC=2，求三棱锥P-EBD的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定

专题：立体几何

分析：（Ⅰ）由PA⊥平面ABCD，得到BD⊥PA，又BD⊥PC，则BD⊥平面PAC，进而有，平面PAC⊥平面EBD．
（Ⅱ）

解答： 解：（Ⅰ）因为PA⊥平面ABCD，所以PA⊥BD．
又BD⊥PC，所以BD⊥平面PAC，
因为BD?平面EBD，所以平面PAC⊥平面EBD．
（Ⅱ）由（Ⅰ）可知，BD⊥AC，所以ABCD是菱形，∠BAD=120°．
所以S_△ABD=

1

2

BD•

1

2

AC=

3

．
设AC∩BD=O，连结OE，则（Ⅰ）可知，BD⊥OE．
所以S_△EBD=

1

2

BD•OE=

6

．
设三棱锥P-EBD的高为h，则

1

3

S_△EBD•h=

1

3

S_△ABD•AE，即

1

3

×

6

h=

1

3

×

3

×1，解得h=

2

2

．
∴V=

1

3

S△EBD•h=

3

3

．

点评：在本题的体积求解中，由E是PA的中点，可以直接将三棱锥P-EBD的体积转化成三棱锥A-EBD的体积，进而转化成三棱锥E-ABD的体积，这样计算也比较简单．