题目内容
函数f（x）=（x2-2x）ex（e为自然数的底数）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：本题是选择题，可采用排除法进行逐一排除，根据f（0）=0可知图象经过原点，以及根据导函数大于0时原函数单调递增，求出单调增区间，从而可以进行判定．
解答：
解：因为f（0）=（02-2×0）e0=0，排除C；
因为f'（x）=（x2-2）ex，解f'（x）＞0，
所以x∈(-∞，
)或x∈(
，+∞)时f（x）单调递增，排除B，D．
故选A．
因为f'（x）=（x2-2）ex，解f'（x）＞0，
所以x∈(-∞，
| 2 |
| 2 |
故选A．
点评：本题主要考查了利用导数研究函数的单调性，以及函数的图象等基础知识，考查了排除法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知定义域为（-∞，0）∪（0，+∞）的函数f（x）是偶函数，并且在（-∞，0）上是增函数，若f（2）=0，则
＜0的解集是（ ）
| f(x) |
| x |
| A、（-2，0）∪（0，2） |
| B、（-∞，-2）∪（0，2） |
| C、（-∞，-2）∪（2，+∞） |
| D、（-2，0）∪（2，+∞） |
身高与体重有关系可以用（ ）分析来分析．
| A、残差 | B、回归 |
| C、二维条形图 | D、独立检验 |
设f（x）与g（x）是定义在同一区间[m，n]上的两个函数，若函数y=f（x）+g（x）在x∈[m，n]上有两个不同的零点，则称f（x）和g（x）在[m，n]上是“相互函数”；若f（x）=-4lnx-5x与g（x）=x2+3x+a在区间[1，e]上是相互函数，则a的取值范围为（ ）
| A、[1，4ln2） |
| B、[-e2+2e+4，4ln2） |
| C、（4ln2，+∞） |
| D、[1，-e2+2e+4] |
函数y=-xcsx的图象，只可能是下列各图中的（ ）
A、 |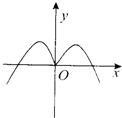
B、 |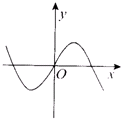
C、 |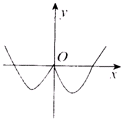
D、 |
边长为2的菱形ABCD中，∠A=60°，沿BD折成直二面角，过点A作PA⊥平面ABC，且AP=2