题目内容
12.在△ABC中,BC=6,M1,M2分别为边BC,AC的中点,AM1与BM2相交于点G,BC的垂直平分线与AB交于点N,且$\overrightarrow{NG}$•$\overrightarrow{NC}$-$\overrightarrow{NG}$•$\overrightarrow{NB}$=6,则$\overrightarrow{BA}$•$\overrightarrow{BC}$=36.分析 由$\overrightarrow{NG}$•$\overrightarrow{NC}$-$\overrightarrow{NG}$•$\overrightarrow{NB}$=6得$\overrightarrow{NG}•\overrightarrow{BC}=6$.用$\overrightarrow{BA}$,$\overrightarrow{N{M}_{1}}$,$\overrightarrow{BC}$表示出$\overrightarrow{NG}$,列方程解出$\overrightarrow{BA}•\overrightarrow{BC}$.
解答 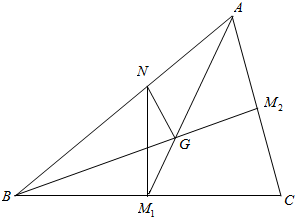 解:∵$\overrightarrow{NG}$•$\overrightarrow{NC}$-$\overrightarrow{NG}$•$\overrightarrow{NB}$=6,∴$\overrightarrow{NG}•\overrightarrow{BC}=6$.
解:∵$\overrightarrow{NG}$•$\overrightarrow{NC}$-$\overrightarrow{NG}$•$\overrightarrow{NB}$=6,∴$\overrightarrow{NG}•\overrightarrow{BC}=6$.
∵M1,M2分别为边BC,AC的中点,∴G是△ABC的重心.
∴$\overrightarrow{{M}_{1}G}=\frac{1}{3}\overrightarrow{{M}_{1}A}=\frac{1}{3}\overrightarrow{BA}-\frac{1}{3}\overrightarrow{B{M}_{1}}$,
∴$\overrightarrow{NG}=\overrightarrow{N{M}_{1}}+\overrightarrow{{M}_{1}G}$=$\overrightarrow{N{M}_{1}}+\frac{1}{3}\overrightarrow{BA}-\frac{1}{3}\overrightarrow{B{M}_{1}}$,
∴($\overrightarrow{N{M}_{1}}+\frac{1}{3}\overrightarrow{BA}-\frac{1}{3}\overrightarrow{B{M}_{1}}$)$•\overrightarrow{BC}$=6.
即$\overrightarrow{N{M}_{1}}•\overrightarrow{BC}$+$\frac{1}{3}\overrightarrow{BA}•\overrightarrow{BC}$-$\frac{1}{3}\overrightarrow{B{M}_{1}}•\overrightarrow{BC}$=6.
∵NM1⊥BC,BM1=3,BC=6,
∴$\overrightarrow{N{M}_{1}}•\overrightarrow{BC}=0$,$\overrightarrow{B{M}_{1}}•\overrightarrow{BC}=3×6$=18.
∴$\frac{1}{3}$$\overrightarrow{BA}•\overrightarrow{BC}$-6=6,
∴$\overrightarrow{BA}•\overrightarrow{BC}$=36.
故答案为36.
点评 本题考查了平面向量加减运算的几何意义,平面向量数量积运算,属于中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | (-∞,4] | B. | (0,4] | C. | (-4,0] | D. | [0,+∞) |
 在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.
在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.