题目内容
2.设函数f(x)=|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )| A. | (-∞,4] | B. | (0,4] | C. | (-4,0] | D. | [0,+∞) |
分析 由题意求出f(x)的值域,再把对任意x1∈R,都存在x2∈R,使f(x1)=g(x2)转化为函数g(x)的值域包含f(x)的值域,进一步转化为关于a的不等式组求解.
解答 解:?x1∈R,f(x)=|x|∈[0,+∞),
∵?x2∈R,使f(x1)=g(x2),
∴g(x)=lg(ax2-4x+1)的值域包含[0,+∞),
当a=0时,g(x)=lg(-4x+1),显然成立;
当a≠0时,要使g(x)=lg(ax2-4x+1)的值域包含[0,+∞),
则ax2-4x+1的最小值小于等于1,
∴$\left\{\begin{array}{l}{a>0}\\{\frac{4a-(-4)^{2}}{4a}≤1}\end{array}\right.$,即a>0.
综上,a≥0.
∴实数a的取值范围是[0,+∞).
故选:D.
点评 本题考查函数的值域,体现了数学转化思想方法,正确理解题意是解答该题的关键,是中档题.

练习册系列答案
相关题目
13.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-3≤0}\\{y≥1}\end{array}\right.$若目标函数z=2x+y的最小值为a,最大值为b,则函数y=x-$\frac{4}{x}$在[a,b]上的值域为( )
| A. | (-∞,3) | B. | [3,$\frac{21}{5}$]. | C. | [-3,3] | D. | [5,+∞) |
10.若函数f(x)=2sin(4x+φ)(φ<0)的图象关于直线x=$\frac{π}{24}$对称,则φ的最大值为( )
| A. | -$\frac{5π}{3}$ | B. | -$\frac{2π}{3}$ | C. | -$\frac{π}{6}$ | D. | -$\frac{5π}{6}$ |
17.已知$cos2α=\frac{3}{7}$且cosα<0,tanα<0,则sinα等于( )
| A. | $-\frac{{\sqrt{14}}}{7}$ | B. | $\frac{{\sqrt{14}}}{7}$ | C. | $-\frac{{2\sqrt{7}}}{7}$ | D. | $\frac{{2\sqrt{7}}}{7}$ |
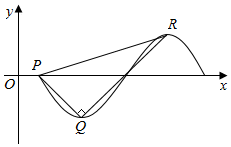 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )