题目内容
10.在平面直角坐标系xOy中,以原点O为极点,以x轴的正半轴为极轴建立极坐标系,设曲线C的极坐标方程为ρ(1+cos2θ)=8sinθ,直线l的参数方程为$\left\{\begin{array}{l}{x=-2a+t}\\{y=3a-t}\end{array}\right.$ (t为参数).(I)求曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C相切,求直线l与两坐标轴围成的三角形的面积.
分析 (I)利用二倍角公式化简极坐标方程,再根据极坐标与直角坐标的对应关系得出曲线C的直角坐标方程;
(II)将直线l的参数方程代入曲线C的普通方程得到关于参数t的一元二次方程,令△=0解出a,得到直线l的方程,求出直线l与坐标轴的交点坐标,计算三角形面积.
解答 解:(I)∵曲线C的极坐标方程为ρ(1+cos2θ)=8sinθ,
∴2ρcos2θ=8sinθ,
∴ρ2cos2θ=4ρsinθ.
∴曲线C的直角坐标方程为x2=4y.
(II)将直线l的参数方程代入曲线C的普通方程得:t2+(4-4a)t+4a2-12a=0.
∵直线l与曲线C相切,
∴△=(4-4a)2-4(4a2-12a)=0,解得a=-1.
∴直线l的普通方程为x+y=-1.
∴直线l与坐标轴的交点为(0,-1),(-1,0).
∴直线l与两坐标轴围成的三角形的面积为S=$\frac{1}{2}×1×1=\frac{1}{2}$.
点评 本题考查了极坐标方程与直角坐标方程的转化,参数方程的应用,属于中档题.

练习册系列答案
相关题目
1.若集合A={x|x2-2x-3>0},集合B={x|3x>8},则A∩B等于( )
| A. | (-1,3) | B. | (-∞,-1) | C. | (3,+∞) | D. | (log38,+∞) |
 ,记
,记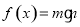 .
. 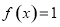 ,求
,求 的值;
的值;  中,角
中,角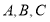 的对边分别是
的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.