题目内容
16.在复平面上复数-3-2i,-4+5i,2+i所对应的点分别是A、B、C,则平行四边形ABCD的对角线BD所对应的复数是7-11i.分析 由题意画出图形,根据A,B,C所对应的复数分别为-3-2i、-4+5i、2+i,得到$\overrightarrow{BA}$、$\overrightarrow{BC}$所对应的复数,然后利用向量加法求得BD所对应的复数.
解答 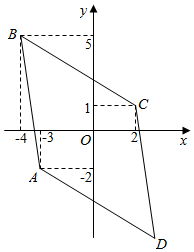 解:如图,
解:如图,
∵A,B,C所对应的复数分别为-3-2i、-4+5i、2+i,
∴$\overrightarrow{BA}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$=(-3-2i)-(-4+5i)=1-7i,
$\overrightarrow{BC}$=$\overrightarrow{OC}$-$\overrightarrow{OB}$=(2+i)-(-4+5i)=6-4i,
$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{BC}$=(1-7i)+(6-4i)=7-11i.
故答案为:7-11i.
点评 本题考查复数的代数表示法及其几何意义,考查了复数的加减法运算,是基础的计算题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
4.已知定义在R上的函数y=f(x)的导函数为f′(x),且满足f′(x)<f(x),f(0)=1,则不等式$\frac{f(x)}{{e}^{x}}$<1的解集为( )
| A. | (-∞,e4) | B. | (e4,+∞) | C. | (-∞,0) | D. | (0,+∞) |
1.甲同学练习投篮,每次投篮命中的概率为$\frac{1}{3}$,如果甲投篮3次,则甲至多有1次投篮命中的概率为( )
| A. | $\frac{20}{27}$ | B. | $\frac{4}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{1}{27}$ |
5.若z∈C,则“|Rez|≤1,|Imz|≤1”是“|z|≤1”成立的 条件.( )
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既非充分又非必要 |
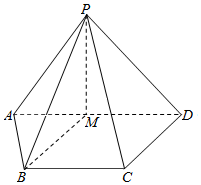 如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.
如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.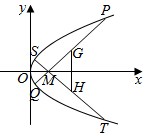 已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线C上的点,且|$\overrightarrow{DF}$|=3.
已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线C上的点,且|$\overrightarrow{DF}$|=3.