题目内容
10. 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 广告投入x/万元 | 1 | 2 | 3 | 4 | 5 |
| 销售收益y/万元 | 2 | 3 | 2 | 5 | 7 |
(Ⅱ)该公司按照类似的研究方法,测得另外一些数据,并整理得到上表:表中的数据显示x与y之间存在线性相关关系,求y关于x的回归方程;
(Ⅲ)若广告投入6万元时,实际销售收益为7.3万元,求残差$\hat e$.
附:${\;}_{b}^{∧}$=$\frac{\sum_{i=1}^{n}{(x}_{i}{-}_{x}^{-}){(y}_{i}{-}_{y}^{-})}{\sum_{i=1}^{n}{(x}_{i}{-}_{x}^{-})^{2}}$=$\frac{\sum_{i=1}^{n}{{x}_{i}y}_{i}-{{n}_{x}^{-}}_{y}^{-}}{\sum_{i=1}^{n}{x}_{i}^{2}-{{n}_{x}^{-}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (Ⅰ)利用频率和为1列方程求出a的值;
(Ⅱ)计算平均数与回归系数,写出线性回归方程;
(Ⅲ)计算x=6时销售收益预测值,再求出残差值.
解答 解:(Ⅰ)设各小长方形的宽度为a,由频率直方图各小长方形的面积总和为1,
可知(0.08+0.1+0.14+0.12+0.04+0.02)•a=0.5a=1,
解得a=2;…(2分)
(Ⅱ)由题意,可知
$\overline{x}=\frac{1+2+3+4+5}{5}=3,\overline{y}=\frac{2+3+2+5+7}{5}=3.8$,
$\sum_{i=1}^5{{x_i}{y_i}=1×2+2}×3+3×2+4×5+5×7=69,\sum_{i=1}^5{x_i^2={1^2}+{2^2}}+{3^2}+{4^2}+{5^2}=55$,…(5分)
根据公式,可求得$\hat b=\frac{69-5×3×3.8}{{55-5×{3^2}}}=\frac{12}{10}=1.2,\hat a=3.8-1.2×3=0.2$,
所以y关于x的回归方程为$\hat y=1.2x+0.2$;…(8分)
(Ⅲ)当x=6时,销售收益预测值为$\hat y=1.2×6+0.2=7.4$(万元),
又实际销售收益为7.3万元,
所以残差$\hat e=7.3-7.4=-0.1$.…(12分)
点评 本题可惜了频率分布直方图与线性回归方程和残差的计算问题,是综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若数列{an}满足a1=1,log2an+1=log2an+1(n∈N*),它的前n项和为Sn,则Sn=( )
| A. | 2-21-n | B. | 2n-1-1 | C. | 2n-1 | D. | 2-2n-1 |
1.圆x2+y2-6x+4y=3的圆心坐标与半径是( )
| A. | $(-3,2)\;\;\;\;\;\;\;\sqrt{13}$ | B. | $(3,-2)\;\;\;\;\;\;\;\sqrt{13}$ | C. | (-3,2)4 | D. | (3,-2)4 |
2.已知($\frac{1}{2}$)a<($\frac{1}{2}$)b<1,则下列不等式成立的是( )
| A. | (a-1)2>(b-1)2 | B. | lna>lnb | C. | a+b>1 | D. | $\sqrt{a}$<$\sqrt{b}$ |
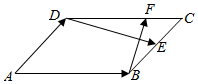 如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;
如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;