题目内容
1.函数f(x)为区间(-∞,0)∪(0,+∞)上的奇函数,且(0,+∞)为增区间,若f(-1)=0,则当$\frac{f(x)}{x}$<0时,x的取值范围是( )| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
分析 根据函数为奇函数,得到在区间(-∞,0)上单调递增,再利用f(1)=0,得到f(-1)=0,从而得到相应的结果.
解答 解:∵函数f(x)奇函数,在区间(0,+∞)上单调递增,
∴在区间(-∞,0)上单调递增,
∵f(-1)=0,
∴f(1)=0,
∴当x<-1时,f(x)<0,
当-1<x<0时,f(x)>0,
当0<x<1时,f(x)<0,
当x>1时,f(x)>0,
∴当-1<x<0或0<x<1时,$\frac{f(x)}{x}$<0,
故选C.
点评 本题考查了函数的奇偶性,函数的单调性,奇函数对称区间上单调性性质的应用,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.已知等差数列{an}的公差d=2,a3=5,数列{bn},bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,则数列{bn}的前10项的和为( )
| A. | $\frac{10}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{19}$ | D. | $\frac{20}{19}$ |
12.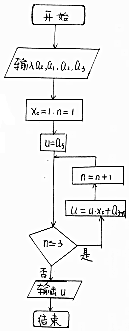 如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
 如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
9.在空间中,下列命题错误的是( )
| A. | 过直线外一点有且只有一条直线与已知直线平行 | |
| B. | 不公线的三个点确定一个平面 | |
| C. | 如果两条直线垂直于同一条直线,那么这两条直线平行 | |
| D. | 如果两个平面垂直于同一个平面,那么这两个平面可能互相垂直 |
6.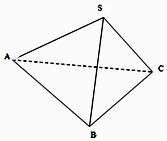 如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
 如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.已知x0是函数f(x)=lnx-6+2x的零点,则下列四个数中最小的是( )
| A. | lnx0 | B. | $ln\sqrt{x_0}$ | C. | ln(lnx0) | D. | ${(ln{x_0})^2}$ |