题目内容
5.直线l与平面α有公共点,则有( )| A. | l∥α | B. | l?α | C. | l与α相交 | D. | l?α或l与α相交 |
分析 利用空间中直线与平面的位置关系进行判断.
解答 解:当直线l∥平面α时,l与平面a无公共点;
当直线l?平面α时,l与平面a有无数个公共点;
当直线l与平面α相交时,l与平面a有一个公共点.
∴若直线l与平面a有公共点,
则l与平面a的位置关系是l?α或l与α相交.
故选D.
点评 本题考查直线与平面的位置关系的判断,解题时要认真审题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知x0是函数f(x)=lnx-6+2x的零点,则下列四个数中最小的是( )
| A. | lnx0 | B. | $ln\sqrt{x_0}$ | C. | ln(lnx0) | D. | ${(ln{x_0})^2}$ |
14.与函数y=x-1-(x-2)0表示同一个函数的是( )
| A. | y=x-2 | B. | $y=\frac{{{x^2}-4}}{x+2}$ | C. | $y=\frac{{{{({x-2})}^2}}}{x-2}$ | D. | $y={({\frac{x-2}{{\sqrt{x-2}}}})^2}$ |
15.已知函数f(x)的定义域为R,f′(x)为函数f(x)的导函数,当x∈[0.+∞)时,2sinxcosx-f′(x)>0且?x∈R,f(-x)+f(x)+cos2x=1.则下列说法一定正确的是( )
| A. | $\frac{1}{4}$-f(-$\frac{5π}{6}$)>$\frac{3}{4}$-f(-$\frac{2π}{3}$) | B. | $\frac{1}{4}$-f(-$\frac{5π}{6}$)>$\frac{3}{4}$-f(-$\frac{4π}{3}$) | ||
| C. | $\frac{3}{4}$-f($\frac{π}{3}$)>$\frac{1}{2}$-f($\frac{3π}{4}$) | D. | $\frac{1}{2}$-f(-$\frac{3π}{4}$)>$\frac{3}{4}$-f($\frac{π}{3}$) |
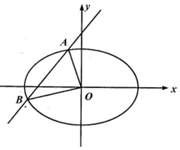 如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.
如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.