题目内容
为了得到y=cos4x,x∈R的图象,只需把余弦曲线上所有点的( )
| A、横坐标伸长到原来的4倍,纵坐标不变 | ||
B、横坐标伸长到原来的
| ||
| C、纵坐标伸长到原来的4倍,横坐标不变 | ||
D、纵坐标伸长到原来的
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:由伸缩变换知,余弦曲线上的所有点横坐标伸长到原来的
倍,纵坐标不变可得y=cos4x,x∈R的图象.
| 1 |
| 4 |
解答:
解:y=cosx
y=cos4x,
故选B.
横坐标伸长到原来的
| ||
故选B.
点评:本题考查了三角函数的伸缩变换的应用,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
4名同学要在同一天上、下午到实验室做A,B,C,D,E五个操作实验,每个同学上下午各做一个实验,且不重复,若上午不能做D实验,下午不能做E实验,则不同的安排方式共有( )
| A、144种 | B、192种 |
| C、216种 | D、264种 |
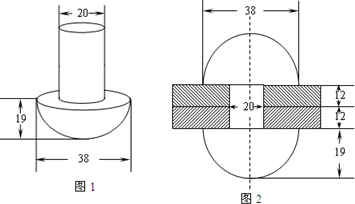 如图,在两块钢板上打孔,用顶帽呈半球形,钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一段每打出一个帽,使得与顶帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2(单位:mm)(加工中不计损失).
如图,在两块钢板上打孔,用顶帽呈半球形,钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一段每打出一个帽,使得与顶帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2(单位:mm)(加工中不计损失).