题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{2^x},(x<1)\\ f(x-1),(x≥1)\end{array}$,则f(log29)的值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{9}{8}$ |
分析 由已知利用分段函数性质及对数函数性质能求出f(log29)的值.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{2^x},(x<1)\\ f(x-1),(x≥1)\end{array}$,
∴f(log29)=f(log29-3)
=${2}^{lo{g}_{2}9}$÷23
=$\frac{9}{8}$.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数性质及对数函数性质的合理运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
15.方程2x=x+1的解的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.甲、乙两人在5次体育测试中成绩见下表,其中●表示一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$.
| 甲 | 89 | 91 | 90 | 88 | 92 |
| 乙 | 83 | 87 | 9● | 83 | 99 |
20.实数x,y满足条件$\left\{\begin{array}{l}2x-y≥0\\ x+y-4≥0\\ x≤3.\end{array}\right.$,则$\frac{y^2}{x^2}$的取值范围为( )
| A. | [4,+∞) | B. | $[\frac{1}{3},2]$ | C. | [0,4] | D. | $[\frac{1}{9},4]$ |
17.已知等差数列{an}中,若a3+3a6+a9=120,则2a7-a8的值为( )
| A. | 24 | B. | -24 | C. | 20 | D. | -20 |
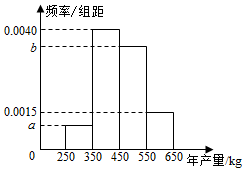 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.