题目内容
1.已知四边形ABCD的边长分别为AB=1,BC=3,CD=DA=2,且A+C=180°,则四边形ABCD的面积为2$\sqrt{3}$.分析 连结BD,根据余弦定理列出方程解出sinA,代入面积公式即可.
解答 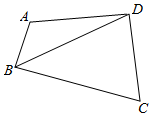 解:连结BD,在△ABD中,BD2=AB2+AD2-2AB•ADcosA=5-4cosA,
解:连结BD,在△ABD中,BD2=AB2+AD2-2AB•ADcosA=5-4cosA,
在△BCD中,BD2=BC2+CD2-2BC•CDcosC=13-12cosC.
∴5-4cosA=13-12cosC,
∵A+C=180°,∴cosA=-cosC.
∴cosA=-$\frac{1}{2}$.
∴sinA=sinC=$\frac{\sqrt{3}}{2}$.
∴四边形ABCD的面积S=S△ABD+S△BCD=$\frac{1}{2}AB×AD×sinA$+$\frac{1}{2}BC×CD×sinC$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
11.执行如图所示的程序框图,输出的i为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
12.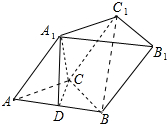 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
(1)求证:平面A1CD⊥平面A1AB;
(2)求二面角A1-BC-C1的余弦值.
 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.(1)求证:平面A1CD⊥平面A1AB;
(2)求二面角A1-BC-C1的余弦值.
9.过曲线y=$\frac{1}{8}$x4上一点P(2,2)的切线的斜率是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
11.在区间(0,+∞)上,函数y=lg(1+$\frac{1}{x}$)是( )
| A. | 增函数,且y>0 | B. | 增函数,且y<0 | C. | 减函数,且y>0 | D. | 减函数,且y<0 |