题目内容
7.已知α为第四象限角且$\sqrt{1-sinα}$+$\sqrt{1+sinα}$=$\sqrt{3}$,则sin($\frac{π}{2}$+α)•cos($\frac{π}{2}$+α)=$\frac{\sqrt{3}}{4}$.分析 对$\sqrt{1-sinα}$+$\sqrt{1+sinα}$=$\sqrt{3}$两边平方化简得出cosα,利用α的象限得出sinα,再利用诱导公式化简得出答案.
解答 解:∵α为第四象限角,∴sinα<0,cosα>0.
∵$\sqrt{1-sinα}$+$\sqrt{1+sinα}$=$\sqrt{3}$,∴1-sinα+1+sinα+2$\sqrt{1-si{n}^{2}α}$=3,
即2+2cosα=3,
∴cosα=$\frac{1}{2}$,sinα=-$\frac{\sqrt{3}}{2}$.
∴sin($\frac{π}{2}$+α)•cos($\frac{π}{2}$+α)=cosα•(-sinα)=$\frac{1}{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题考查了三角函数的恒等变换与化简求值,属于中档题.

练习册系列答案
相关题目
18.为了促进公民通过“走步”健身,中国平安公司推出的“平安好医生”软件,最近开展了“步步夺金”活动.活动规则:①使用平安好医生APP计步器,每天走路前1000步奖励0.3元红包,之后每2000步奖励0.1元红包,每天最高奖励不超过3元红包.②活动期间,连续3天领钱成功,从第4天起走路奖金翻1倍(乘以2),每天最高奖励不超过6元红包.某人连续使用此软件五天,并且每天领钱成功.这五天他走的步数统计如下:
则他第二天获得的奖励红包为1.0元,这五天累计获得的奖励红包为8.0元.
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 | 第五天 |
| 步数 | 13980 | 15456 | 17890 | 19012 | 21009 |
15.已知集合A={x|$\frac{x}{x-2}$≤0},集合B={1,2,3},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {3} |
2.从数字1,2,3,4,5中任取2个,组成一个没有重复数字的两位数,则这个两位数大于30的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.设集合A={-1,0},集合B={0,1,2},则A∪B的子集个数是( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
19.在学生会主席竞选中,要从10名男同学和5名女同学中任意选取两名担任主席,不同的选法有( )
| A. | ${C}_{10}^{1}$•${C}_{5}^{1}$种 | B. | ${A}_{10}^{1}$•${A}_{5}^{1}$种 | C. | ${C}_{15}^{2}$种 | D. | ${A}_{15}^{2}$种 |
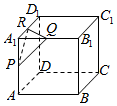 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.