题目内容
17.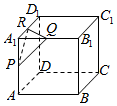 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
分析 分别取过C点的三条面对角线的中点,则此三点为棱柱的另一个底面的三个顶点,利用中位线定理证明.于是三棱柱的高为正方体体对角线的一半.
解答 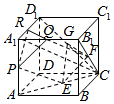 解连结A1C,AC,B1C,D1C,分别取AC,B1C,D1C的中点E,F,G,连结EF,EG,FG.
解连结A1C,AC,B1C,D1C,分别取AC,B1C,D1C的中点E,F,G,连结EF,EG,FG.
由中位线定理可得PE$\stackrel{∥}{=}$A1C,QF$\stackrel{∥}{=}$A1C,RG$\stackrel{∥}{=}$A1C.
又A1C⊥平面PQR,∴三棱柱PQR-EFG是正三棱柱.
∴三棱柱的高h=PE=$\frac{1}{2}$A1C=$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查了正棱柱的结构特征,作出三棱柱的底面是计算棱柱高的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.对于数列{an},定义数列{an+1-an}为数列{an}的“等差列”,若a1=2,{an}的“等差列”的通项公式为2n,则数列{an}的前2015项和S2015=( )
| A. | 22016-1 | B. | 22016 | C. | 22016+1 | D. | 22016-2 |
 某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的实践,绘成的频率分布直方图如图所示,这100名学生中参加实践活动时间在6-10小时内的人数为58.
某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的实践,绘成的频率分布直方图如图所示,这100名学生中参加实践活动时间在6-10小时内的人数为58.