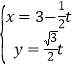题目内容
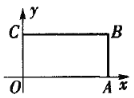
【题目】如图,矩形![]() 为一张台球桌面,
为一张台球桌面,![]() ,
,![]() .从点
.从点![]() 击出一个球,其可无限次经台球桌四边反弹运行.已知该球经过矩形
击出一个球,其可无限次经台球桌四边反弹运行.已知该球经过矩形![]() 的中心
的中心![]() .
.
(1)试求所有整点![]()
![]() 的个数,使得该球可以经过点
的个数,使得该球可以经过点![]() ;
;
(2)若该球在上述![]() 、
、![]() 两点间的最短路径长为
两点间的最短路径长为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将矩形![]() 及点
及点![]() 、
、![]() 整体向右、上方向翻转复制,得到一系列矩形.
整体向右、上方向翻转复制,得到一系列矩形.
设第![]() 列、第
列、第![]() 行矩形中
行矩形中![]() 、
、![]() 的像分别为
的像分别为![]() 、
、![]() .则
.则
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() .则
.则
![]() , ①
, ①
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
故经过点![]() 的球可以经过点
的球可以经过点![]()
![]() 存在
存在![]() 、
、![]() 、
、![]() 、
、![]() ,使得
,使得![]() . ②
. ②
为使式②成立,必须![]() ,
,![]()
![]() .
.
故![]() .
.
(2)下面利用式②验证球可以经过上述点![]() ,并计算
,并计算![]() .
.
对前五个点![]() ,有
,有![]() ,且
,且![]() ,
,
![]() ,
,![]() .
.
对中间四个点![]() ,有
,有![]() ,故球在
,故球在![]() 、
、![]() 之间必须经台球桌四边之一反弹,有
之间必须经台球桌四边之一反弹,有
![]() ,
,
![]() .
.
从而,![]() ,
,
![]() .
.
对![]() ,若球在某一矩形内直接经过
,若球在某一矩形内直接经过![]() 、
、![]() (不必经矩形边反弹),则
(不必经矩形边反弹),则![]() .
.
此时,由式①知![]() ,且
,且![]() .但当
.但当![]() 时,
时,![]() ,矛盾.
,矛盾.
若球在![]() 、
、![]() 之间只反弹一次,则球经过某两个相邻的矩形中的
之间只反弹一次,则球经过某两个相邻的矩形中的![]() 、
、![]() ,有
,有![]() ,但由式①有
,但由式①有![]() ,矛盾.
,矛盾.
故球在![]() 、
、![]() 之间必须经台球桌四边反弹至少两次,有
之间必须经台球桌四边反弹至少两次,有
![]() .
.
从而,![]() .
.
综上,所求整点![]() 有11个,且
有11个,且![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() 得到如图所示的频率分布直方图.
得到如图所示的频率分布直方图.
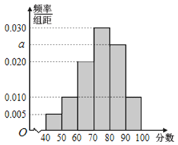
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请在答题卡上将![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
参考公式及数据: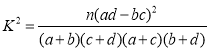 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |