题目内容

6．已知随机变量ξ服从正态分布N（2，σ2），若P（0≤ξ≤2）=0.3，则P（ξ≥4）=（　　）
A．0.2B．0.3C．0.6D．0.8

分析 随机变量ξ的均值为2，根据正态分布的对称性即可得出答案．

解答 解：∵随机变量ξ服从正态分布N（2，σ2），
∴P（ξ≤2）=P（ξ＞2）=0.5，
∵P（0≤ξ≤2）=0.3，∴P（2＜ξ＜4）=0.3，
∴P（ξ＞4）=P（ξ＞2）-P（2＜ξ＜4）=0.2．
故选：A．

点评 本题考查了正态分布的对称性，属于中档题．

练习册系列答案
相关题目
16．已知抛物线C：y2=2px（p＞0）的焦点为F，点M（x0，4）是抛物线C上一点，以M为圆心，|MF|为半径的圆被直线x=-1截得的弦长为2$\sqrt{7}$，则|MF|等于（　　）
A．2B．3C．4D．5
17．如图1，菱形ABCD的对角线AC与BD交于点E，∠BAD=60°，将△BAD折起，使得点A到点A′的位置，点P满足$\overrightarrow{CP}$=λ$\overrightarrow{CA′}$+（1-λ）$\overrightarrow{CE}$．

（1）证明：BD⊥CP；
（2）若λ=$\frac{1}{2}$，二面角A′-BD-C为120°，求直线BP与平面A′CD所成角的正弦值．
14．若x，y满足约束条件$\left\{{\begin{array}{l}{x-y≤0}\\{2x-y≥0}\\{2x+y≤4}\end{array}}\right.$，z=x+y+3与z=x+ny取得最大值的最优解相同，则实数n的取值范围是（　　）
A．{1}B．$（{-∞，\frac{1}{2}}）$C．$（{\frac{1}{2}，+∞}）$D．[1，+∞）
1．已知函数f（x）=$\frac{m}{x}$+xlnx（m＞0），g（x）=lnx-2．
（1）当m=1时，求函数f（x）的单调区间；
（2）设函数h（x）=f（x）-xg（x）-$\sqrt{2}$，x＞0．若函数y=h（h（x））的最小值是$\frac{3\sqrt{2}}{2}$，求m的值；
（3）若函数f（x），g（x）的定义域都是[1，e]，对于函数f（x）的图象上的任意一点A，在函数g（x）的图象上都存在一点B，使得OA⊥OB，其中e是自然对数的底数，O为坐标原点，求m的取值范围．
11．某研究性学习小组调查研究性别对喜欢吃甜食的影响，部分统计数据如表：
  女生 男生 合计
 喜欢吃甜食 8 4 12
 不喜欢吃甜食216 18
 合计 10 20 30
附表：
 P（K2≥k0） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
经计算K2=10，则下列选项正确的是（　　）
A．有99.5%的把握认为性别对喜欢吃甜食无影响
B．有99.5%的把握认为性别对喜欢吃甜食有影响
C．有99.9%的把握认为性别对喜欢吃甜食无影响
D．有99.9%的把握认为性别对喜欢吃甜食有影响
18．若抛物线y2=8x的焦点F与双曲线$\frac{x^2}{3}-\frac{y^2}{n}=1$的一个焦点重合，则n的值为（　　）
A．2B．-1C．1D．4
14．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-1（x≤0）}\\{f（x-1）（x＞0）}\end{array}\right.$，若函数g（x）=f（x）-ax+1有5个不同的零点，则实数α的取值范围是[$\frac{1}{5}$，$\frac{1}{4}$）．
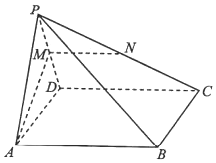15．如图，在四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥平面ABCD，AP=AD，M，N分别为棱PD，PC的中点．求证：
（1）MN∥平面PAB
（2）AM⊥平面PCD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网