题目内容
已知椭圆
+
=1，离心率为
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过a＞4的椭圆的右焦点F任作一条斜率为k（k≠0）的直线交椭圆于A，B两点，问在F右侧是否存在一点D（m，0），连AD、BD分别交直线x=
于M，N两点，且以MN为直径的圆恰好过F，若存在，求m的值；若不存在，请说明理由．
| x2 |
| a2 |
| y2 |
| 16 |
| 3 |
| 5 |
（Ⅰ）求椭圆的方程；
（Ⅱ）过a＞4的椭圆的右焦点F任作一条斜率为k（k≠0）的直线交椭圆于A，B两点，问在F右侧是否存在一点D（m，0），连AD、BD分别交直线x=
| 25 |
| 3 |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）由椭圆
+
=1，离心率为
，易知a=5，可得求椭圆的方程；
（Ⅱ）设AB的方程为y=k（x-3），代入
+
=1，利用韦达定理，结合
•
=0，即可得出结论．
| x2 |
| a2 |
| y2 |
| 16 |
| 3 |
| 5 |
（Ⅱ）设AB的方程为y=k（x-3），代入
| x2 |
| 25 |
| y2 |
| 16 |
| FM |
| FN |
解答：
解：（Ⅰ）由椭圆
+
=1，离心率为
，易知a=5，椭圆的方程为
+
=1或
+
=1 …4分
（Ⅱ）存在m=5，理由如下：由题知，F（3，0）．
设AB的方程为y=k（x-3）．
设A（x1，y1），B（x2，y2），
由直线代入
+
=1，可得（16+25k2）x2-150k2x+225 k2-400=0
∴x1+x2=
，x1x2=
；y1y2=-
----------------------6分
设M（
，y3），N（
，y4），由M、A、D共线，y3=
，同理y4=
…8分
又
=（
，y3），
=（
，y4），由已知得
•
=0得y3y4=-
，
∴
•
=-
，
∴（1+k2）（16m2-400）=0，
∴m=±5，
∵m＞3，∴m=5 …12分
| x2 |
| a2 |
| y2 |
| 16 |
| 3 |
| 5 |
| x2 |
| 25 |
| y2 |
| 16 |
| y2 |
| 16 |
| 25x2 |
| 256 |
（Ⅱ）存在m=5，理由如下：由题知，F（3，0）．
设AB的方程为y=k（x-3）．
设A（x1，y1），B（x2，y2），
由直线代入
| x2 |
| 25 |
| y2 |
| 16 |
∴x1+x2=
| 150k2 |
| 16+25k2 |
| 225k2-400 |
| 16+25k2 |
| 256k2 |
| 16+25k2 |
设M（
| 25 |
| 3 |
| 25 |
| 3 |
| (3m-25)y1 |
| 3(m-x1) |
| (3m-25)y2 |
| 3(m-x2) |
又
| FM |
| 16 |
| 3 |
| FN |
| 16 |
| 3 |
| FM |
| FN |
| 256 |
| 9 |
∴
| (3m-25)y1 |
| 3(m-x1) |
| (3m-25)y2 |
| 3(m-x2) |
| 256 |
| 9 |
∴（1+k2）（16m2-400）=0，
∴m=±5，
∵m＞3，∴m=5 …12分
点评：本题考查直线与圆锥曲线的综合问题，考查椭圆方程，考查韦达定理的运用，属于中档题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
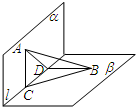已知平面α⊥平面β，α∩β=l，A∈α，B∈β，AC⊥l，垂足为C，BD⊥l，垂足为D（点C，D不重合），若AC＞BD，则（ ）| A、AD＞BC，∠ABC＞∠BAD |
| B、AD＞BC，∠ABC＜∠BAD |
| C、AD＜BC，∠ABC＞∠BAD |
| D、AD＜BC，∠ABC＜∠BAD |
设定义在（0，+∞）的函数f（x）的导函数为f′（x），且满足2f（x）+xf′（x）＞x2．若a，b，c满足a=22.2•f（21.1），b=（log32）2•f（log32），c=（log23）2•f（log23），则a，b，c的大小关系是（ ）
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜a＜b |
| D、b＜c＜a |
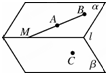如图，α∩β=l，A，B∈α，C∈β，且C∉l，直线AB∩l=M，过A，B，C三点的平面记作γ，则γ与β的交线必通过（ ）| A、点A | B、点B |
| C、点C但不过点M | D、点C和点M |
已知F1，F2是双曲线
-
=1（a＞0，b＞0）的焦点，以线段F1F2为边作正三角形MF1F2，若边MF1的中点在双曲线上，则双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、4+2
| ||||
B、
| ||||
C、
| ||||
D、
|