题目内容
正方体ABCD-A1B1C1D1中,异面直线A1B与AD1所成角的大小为 .
考点:异面直线及其所成的角
专题:计算题,空间位置关系与距离
分析:连接BC1,证明∠A1BC1为异面直线A1B和直线AD1所成的角,在△A1BC1中求∠A1BC1.
解答:
 解:连接A1C1,BC1,∵AD1∥BC1,∴∠A1BC1为异面直线A1B和直线AD1所成的角,
解:连接A1C1,BC1,∵AD1∥BC1,∴∠A1BC1为异面直线A1B和直线AD1所成的角,
∵在正方体ABCD-A1B1C1D1中,设棱长为1,则A1C1=BC1=BA1=
,
∴△A1BC1为等边三角形,∴∠A1BC1=60°
故答案是60°.
 解:连接A1C1,BC1,∵AD1∥BC1,∴∠A1BC1为异面直线A1B和直线AD1所成的角,
解:连接A1C1,BC1,∵AD1∥BC1,∴∠A1BC1为异面直线A1B和直线AD1所成的角,∵在正方体ABCD-A1B1C1D1中,设棱长为1,则A1C1=BC1=BA1=
| 2 |
∴△A1BC1为等边三角形,∴∠A1BC1=60°
故答案是60°.
点评:本题主要考查了空间两异面直线及其所成的角的求法,根据异面直线所成角的定义,寻找平行线是解决本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图甲所示,在正方形ABCD中,EF分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为H,如图乙所示,那么,在四面体A-EFH中必有( )
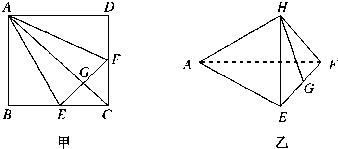

| A、AH⊥△EFH所在平面 |
| B、AG⊥△EFH所在平面 |
| C、HF⊥△AEF所在平面 |
| D、HG⊥△AEF所在平面 |
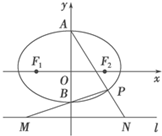 如图,椭圆
如图,椭圆 如图是各棱长均相等的正四棱锥表面展开图,T为QS的中点,则在四棱锥中PQ与RT所成角的余弦值为
如图是各棱长均相等的正四棱锥表面展开图,T为QS的中点,则在四棱锥中PQ与RT所成角的余弦值为 如图,在直三棱柱ABC-A1B1C1中,D、E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.
如图,在直三棱柱ABC-A1B1C1中,D、E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.