题目内容
已知f(t)=log2t,t∈[
,8]对f(t)值域内所有实数m都成立,不等式x2+(m-4)x+4-2m>0恒成立,求x的取值范围.
| 2 |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:由t∈[
,8],得f(t)∈[
,3],x≠2.令g(m)=m(x-2)+(x-2)2,m∈[
,3],问题转化为g(m)在m∈[
,3]上恒大于0,运用一次函数的图象和性质,由此能求出x的取值范围.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵t∈[
,8],∴f(t)∈[
,3]
原题转化为:m(x-2)+(x-2)2>0恒成立,为m的一次函数,
当x=2时,不等式不成立.
∴x≠2.令g(m)=m(x-2)+(x-2)2,m∈[
,3],
问题转化为g(m)在m∈[
,3]上恒大于0,
则:
,即
,即有
.
解得:x>2或x<-1.
则有x的取值范围是(-∞,-1)∪(2,+∞).
| 2 |
| 1 |
| 2 |
原题转化为:m(x-2)+(x-2)2>0恒成立,为m的一次函数,
当x=2时,不等式不成立.
∴x≠2.令g(m)=m(x-2)+(x-2)2,m∈[
| 1 |
| 2 |
问题转化为g(m)在m∈[
| 1 |
| 2 |
则:
|
|
|
解得:x>2或x<-1.
则有x的取值范围是(-∞,-1)∪(2,+∞).
点评:本题考查不等式恒成立问题,是中档题,解题时要注意对数性质的合理运用和构造一次函数,运用图象和性质解题.

练习册系列答案
相关题目
若函数f(x)=x3-3x+m恰有2个不同的零点,则实数m的值为( )
| A、±2 | B、±1 |
| C、-2或1 | D、-1或2 |
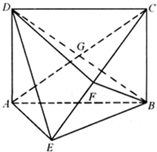 如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.
如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.