题目内容
在三角形ABC中,B=600,AC= , 则AB+2BC的最大值为( )
, 则AB+2BC的最大值为( )
 , 则AB+2BC的最大值为( )
, 则AB+2BC的最大值为( )| A.3 | B. | C. | D.2 |
D
试题分析:设AB="c" AC="b" BC=a利用余弦定理和已知条件求得a和c的关系,设c+2a=m代入,利用判别大于等于0求得m的范围,则m的最大值可得.
设AB="c" AC="b" BC=a
由余弦定理cosB=
 ,所以a2+c2-ac=b2=3
,所以a2+c2-ac=b2=3设c+2a="m" 代入上式得7a2-5am+m2-3=0△=84-3m2≥0 故m≤2

当m=2
 时,此时a=
时,此时a= c=
c= 符合题意,因此最大值为2
符合题意,因此最大值为2 ,故选D
,故选D点评:解决该试题的关键是将所求的边化为角,转化为单一三角函数,借助于角的范围得到
三角函数的值域。

练习册系列答案
相关题目
 中,若
中,若 ,
, ,
, ,则
,则 ( )
( )



 ,则
,则 _________。
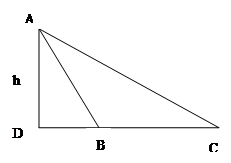
_________。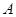 上测得正前方的河流的两岸
上测得正前方的河流的两岸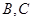 的俯角分别为
的俯角分别为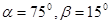 ,如果这时气球的高度
,如果这时气球的高度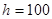 米,求河流的宽度
米,求河流的宽度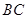 .
.
 中,
中, ,则A等于 ( )
,则A等于 ( )
 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.(1)求
成等差数列.(1)求 的值;(2)求
的值;(2)求 的取值范围。
的取值范围。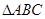 中,
中,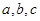 分别是角
分别是角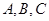 的对边,且
的对边,且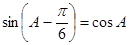 .
.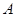 的大小;
的大小;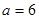 时,求
时,求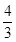
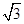 -3
-3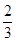
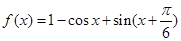 .
.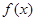 的最小正周期;
的最小正周期;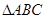 得内角
得内角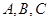 的对应边为
的对应边为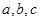 ,若
,若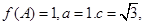 求
求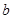 的值.
的值.