题目内容
已知函数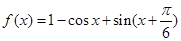 .
.
(Ⅰ)求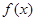 的最小正周期;
的最小正周期;
(Ⅱ)记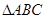 得内角
得内角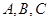 的对应边为
的对应边为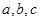 ,若
,若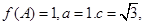 求
求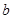 的值.
的值.
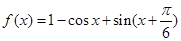 .
.(Ⅰ)求
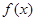 的最小正周期;
的最小正周期;(Ⅱ)记
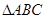 得内角
得内角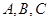 的对应边为
的对应边为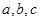 ,若
,若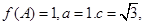 求
求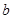 的值.
的值.解:(Ⅰ) 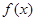 的最小正周期为
的最小正周期为 ;
;
(Ⅱ)


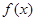 的最小正周期为
的最小正周期为 ;
;(Ⅱ)



本试题主要是考查了三角函数的性质和解三角形的综合运用。
(1)函数 ,化简得到
,化简得到 ,得到周期。
,得到周期。
(2)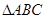 中,
中, ,
,
即 ,所以
,所以 ,结合余弦定理得到参数b的值。
,结合余弦定理得到参数b的值。
(1)函数
 ,化简得到
,化简得到 ,得到周期。
,得到周期。(2)
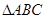 中,
中, ,
, 即
 ,所以
,所以 ,结合余弦定理得到参数b的值。
,结合余弦定理得到参数b的值。
练习册系列答案
相关题目
 , 则AB+2BC的最大值为( )
, 则AB+2BC的最大值为( )
 的三个内角
的三个内角 的对边分别为
的对边分别为 ,已知
,已知 成等比数列,且
成等比数列,且

 的大小;
的大小;  ,求函数
,求函数 的值域.
的值域. 中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2
中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2 -1)=-
-1)=- cos2B.
cos2B. ,求
,求 的最大值.
的最大值. .
. ,求
,求 面积的最大值.
面积的最大值. 
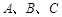 所对的边分别为
所对的边分别为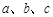 ,边a、b是方程x2-2
,边a、b是方程x2-2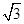 x +2=0的两根,角A、B满足关系2sin(A+B)-
x +2=0的两根,角A、B满足关系2sin(A+B)- 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 ,
, ,
, .求
.求 中,已知a=6,b=8,A=30°,求角B则( ).
中,已知a=6,b=8,A=30°,求角B则( ).